Possible Explanation for the Physical Lorentz Contraction
Doug Marett (2015)
This explanation is for the
physical Lorentz contraction of Hendrik Lorentz and George Fitzgerald, as
distinct from that of Einstein. Einstein did not of course believe that the
Lorentz contraction was physical, but rather believed that it was an effect
dependent on the perspective of the observer. However, in this discussion we
will consider how the Lorentz contraction could actually be a physical effect as
was believed by Lorentz, Fitzgerald, and the Maxwellians. The effect was
originally criticized as being artificial or ad hoc by Popper, serving to restore
agreement between theory and experiment. However, certain findings about the
nature of matter in the 1920’s led to an understanding that would be entirely
compatible with this original premise of a physical contraction of matter with
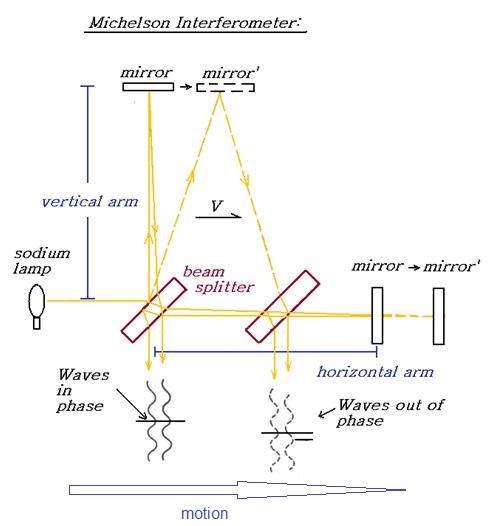
velocity. Consider the propagation time of light in a Michelson interferometer
using Lorentz’s equation incorporating the Fresnel drag coefficient:
The2 way time required for a beam of light to travel
perpendicular to its direction of travel at velocity V with respect to a
preferred frame is: 2T = 2 x [D/(C/n –
W/n^2)] Or If n=1, then 2T =
2D/C x 1/(SQRT(1-v^2/c^2)) see: ref The 2-way time required for a beam of light to travel
parallel under the same conditions is: 2T= D/(C/n+ v/n^2)+
D/(C/n- v/n^2) Or If n =1, then 2T =
2D/C x (1 + v^2/C^2) see: ref Where: D = the one way path
length V = velocity through
space n = refractive index of
arms C = speed of light in space W = transverse velocity component C –
SQRT(C^2 – v^2) The parallel beam transit time is found to be slower than
the perpendicular by the factor 1/SQRT(1-V^2/C^2) (The Lorentz
factor) The hypothesis put forward by
Fitzgerald and Lorentz was that the apparatus must contract in the parallel
direction by this factor to nullify the result.
But why would matter contract in the direction of motion when it
experiences a velocity?
All we have to do is consider that atoms and other particles behave just
like waves, and have dimensions based on their wavelength (including their bond
lengths). Evidence has long suggested that atoms and particles are composed of
waves, have a wavelength and a frequency, akin to photons. As is well known,
electrons fired through a Young double slit will interfere with one another,
just like waves of light. When Schrodinger developed his model of the atom and
atomic orbitals, he was building on De Broglie’s hypothesis that particles had
a wavelike essence. Schrodinger’s model, which correctly predicted the shape of
atomic orbitals, was based on modelling how electromagnetic waves could be
constrained to form a stable 3D structure in space. This is why when
Schrodinger first invented Quantum Mechanics, he called it “Wave Mechanics.” Schrodinger
was an expert in hydrodynamics, the motion of fluids, which is what made him
ideally situated for figuring out the orbital problem. If the reader can accept
the notion that the dimensions of matter and particles depend upon their
wavelength in the vein intended by the two Nobel Laureates above, and that this
wavelength depends upon the speed of light, then it is simply a matter of
investigating how these wavelengths would be expected to change with motion in
order to understand what the physical
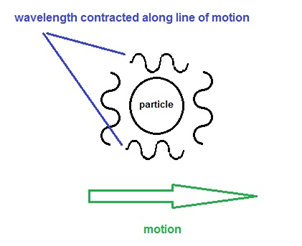
Lorentz contraction really is. We know that the equation C= fl governs the properties of light - we apply
this also to particles. If we consider a beam of light crossing to and fro the
breadth and width of a particle moving at some velocity v, the time to pass
perpendicular and parallel to its motion will be identical to that for the
Michelson interferometer discussed above. Since the apparent speed of light C’
is slower along the parallel path in as measured in the moving frame, if C goes
down, then following C= fl the
wavelength l must contract to compensate.
(Frequency cannot change as this is thermodynamically impossible) And since C
slows down in the moving frame on average by the factor: C’ = C x SQRT (1-V^2/C^2) then the wavelength of the moving
particles or atoms must also contract by the same factor l’ = l
x SQRT (1-V^2/C^2) as measured in the moving frame
of the particle, in the direction of motion. Since an atom’s size and bond
length should be defined by its wavelength, if its wavelength is shorter in the
direction of motion than perpendicular to it, then the moving matter will
contract exactly as predicted by FitzGerald and Lorentz. This is only true of
course if an atom is composed of waves and moves with respect to a preferred
frame of reference for these waves. Proof
of the existence of a physical Lorentz contraction would then give credence to
these two former conditions.
Any attempt to measure anisotropy
in the speed of light in this manner will be impossible, since both the matter
and the laser light will experience a wavelength contraction that will cancel
out around the interferometer. This provides an alternative explanation for why
no Michelson Morley type interferometer experiment has ever been able to detect
our motion through space, because this effect will lead the moving observer to erroneously
measure the speed of light to be equal in all directions, regardless of this
motion. Note: Schrodinger’s wave model of
the atom was overruled by the Copenhagen Interpretation of Quantum Mechanics,
largely due to the pressure of Niels Bohr. Perhaps a wave-mechanical atom was
too much for the particle-ists. Schrodinger was vehemently against this
re-interpretation of his work, saying: Let me say at the outset, that in this discourse, I am
opposing not a few special statements of quantum physics held today (1950s), I
am opposing as it were the whole of it, I am opposing its basic views that have
been shaped 25 years ago, when Max
Born put forward his probability
interpretation, which was accepted by almost everybody. (Schrödinger E, The
Interpretation of Quantum Physics. Ox Bow Press, Woodbridge, CN, 1995). De Broglie
– Nobel
Prize in Physics – 1929 Erwin
Schrodinger – Nobel
Prize in Physics - 1933 |