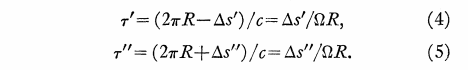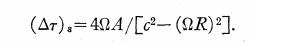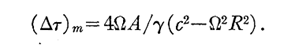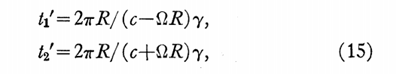L'expérience Sagnac: contredit-il la relativité?

L'expérience Sagnac: contredit-il la relativité?

Par Doug Marett 2012

Un certain nombre d'auteurs ont suggéré que l'effet Sagnac contredit les postulats originaux de la Relativité Spéciale, puisque le postulat de la constance de la vitesse de la lumière est violé dans les systèmes en rotation. [1,2,3] Sagnac lui-même a conçu l'expérience de 1913 pour prouver l'existence de l'éther [4]. D'autres auteurs ont tenté d'expliquer l'effet dans le cadre théorique de la relativité, allant même jusqu'à qualifier l'effet de «relativiste» [5]. Cependant, nous cherchons dans cet article à montrer comment l'effet Sagnac contrevient en principe au concept de la relativité du temps et du mouvement. Pour comprendre comment cela se passe et ses implications plus larges, il faut d'abord regarder le concept du mouvement absolu par rapport au mouvement relatif, ce que l'effet Sagnac implique sur ces mouvements et ce qui suit logiquement les notions plus larges de l'espace et du temps.

Premières idées concernant la rotation et le mouvement absolu:

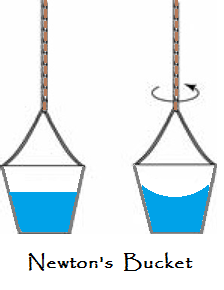
Sir Isaac Newton a d'abord souligné la distinction fondamentale entre mouvement translationnel et mouvement de rotation, et plus tard Ernest Mach et Heinrich Hertz. L'une des premières expériences sur le sujet fut l'expérience de Newton sur le godet de 1689. Il s'agissait d'une expérience pour démontrer que le vrai mouvement de rotation ne peut être défini comme rotation relative d'un corps par rapport aux corps environnants. espace absolu à la place. Dans l'expérience de Newton, un seau est rempli d'eau et accroché par une corde. Si la corde est tordue jusqu'à ce qu'elle soit serrée puis relâchée, le godet commence à tourner rapidement, non seulement par rapport aux observateurs qui le regardent, mais aussi par rapport à l'eau contenue dans le godet. bouge et reste à plat sur sa surface.

Finalement, comme le seau continue à tourner, l'eau commence à tourner aussi, comme on peut le voir à partir de la forme concave de sa surface. Cette concavité de l'eau montre qu'elle tourne, même si elle est maintenant au repos par rapport au godet co-rotatif. Newton a souligné que ce n'est pas le mouvement relatif du seau et de l'eau qui provoque la concavité de l'eau. La concavité de l'eau suggère qu'elle tourne par rapport à quelque chose d'autre, beaucoup plus éloigné. Dans la pensée de Newton, cela montre une rotation par rapport à dire ... l'espace absolu. Ceci est contraire à l'idée que les mouvements ne peuvent être que relatifs.

Maintenant, un observateur assis dans le seau et tournant ainsi avec lui peut voir que l'eau est concave mais ne peut pas voir ou sentir qu'il tourne par rapport à l'environnement, donc la cause de la concavité peut ne pas être évidente surtout si la rotation est lente et que la vue sur les environs est bloquée. D'autre part, un observateur qui se tient près du seau (stationnaire) verra une forme concave de la surface de l'eau qui est cohérente avec son observation du seau tournant devant lui. Ainsi, bien que les deux observateurs voient l'effet de la rotation (surface concave), ils ne peuvent pas nécessairement s'entendre sur la cause.

On dit parfois que parce qu'on peut identifier un cadre immobile (l'observateur près du seau), il n'y a pas de raison de demander "tourner par rapport à quoi?" Cependant, nous voulons montrer que bien que plusieurs cadres fixes puissent être identifiés en fonction de les circonstances, il n'y a qu'un seul cadre stationnaire vraiment unique, et c'est le cadre de l'espace absolu, alias "les étoiles fixes".

L'effet Sagnac:

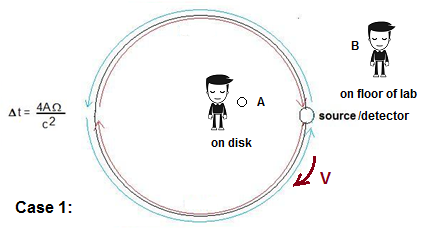
Alors qu'au départ ces idées étaient appliquées aux effets mécaniques, avec l'effet Sagnac, il devient clair que les mêmes principes s'appliquent à la lumière, et le cadre de référence dans lequel la vitesse de la lumière peut être montrée (ou non montrée) constante. Considérons l'effet Sagnac dans le contexte de l'expérience du seau de Newton. Au lieu d'un seau rotatif, nous avons un disque rotatif, et sur le bord du disque deux chemins lumineux provenant d'une source, l'un tournant dans le sens des aiguilles d'une montre et l'autre tournant dans le sens contraire des aiguilles d'une montre. où leur temps de vol est mesuré. Comme le temps de transit est généralement très faible, les différences de temps de retour sont déterminées par une différence de phase entre les deux faisceaux de retour. Pour l'effet Sagnac, nous appelons ce cas 1. La vitesse de la lumière (C) dans le cadre stationnaire est supposée être C ~ = 3 x 10^8 m / s.

Si nous faisons maintenant tourner le disque dans le sens des aiguilles d'une montre à la vitesse v, nous constatons que le faisceau bleu arrive au détecteur avant le faisceau rouge - en fait, la différence de vitesse de la lumière

e révèle être 2 * v, parce que le faisceau bleu se déplace à C + v et le faisceau rouge à C-v. Tout comme l'eau concave, tous les observateurs s'accordent pour dire que le faisceau bleu est arrivé avant le faisceau rouge, mais encore une fois, comme dans le cas du seau de Newton, l'explication de pourquoi dépend de la perspective de l'observateur. Pour l'observateur B, il apparaît que le détecteur s'est approché du faisceau bleu venant en sens inverse et a reculé du faisceau rouge, et c'est le changement de longueur du trajet par rapport aux deux faisceaux qui explique la différence apparente de la vitesse de la lumière. D'autre part, l'observateur de A qui tourne avec le disque a observé que la source et le détecteur sont stationnaires de sa perspective, de même que les chemins, de sorte qu'il ne peut que conclure (sans présumer qu'il tourne) que la lumière a effectivement voyagé à deux vitesses différentes autour du disque, soit C + v et C - v. Qui a raison? Eh bien, le problème est le suivant: du point de vue de la relativité restreinte, il n'y a pas de cadres de référence, il n'y a que des cadres de référence relatifs, donc nous ne pouvons pas soutenir que le cadre B est meilleur que le cadre A prémisse de la théorie. En relativité restreinte (SR), la position de l'observateur est supposée être arbitraire. Cependant, si nous acceptons cette perspective A est légitime, nous rejetons le premier postulat de SR, à savoir:

"Cette lumière est toujours propagée dans l'espace vide avec une vitesse définie c qui est indépendante de l'état de mouvement du corps émetteur". - Einstein [7]

En outre, sur la notion relativiste qu '«il est impossible de détecter le mouvement en mesurant les différences de vitesse de la lumière», comme l'avait apparemment démontré l'expérience Michelson-Morley, l'expérience Sagnac montre que cela peut être fait. En outre, l'observateur A peut déterminer que c'est lui qui tourne, et non son environnement.

Maintenant, pour aborder l'idée des états stationnaires, nous devons poser la question suivante: Y a-t-il un seul observateur unique (cadre de référence) pour lequel la vitesse de la lumière est toujours constante dans un interféromètre de Sagnac? En fait, la vitesse de la lumière mesurée par l'observateur B n'est pas non plus exactement constante, une énigme que nous allons expliquer ci-dessous.

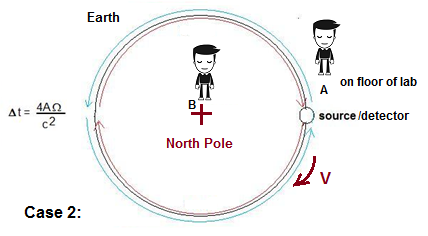
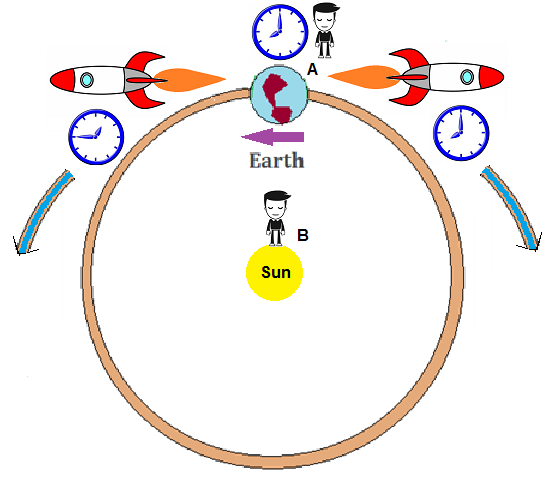
Dans le cas 1, nous rappelons que l'observateur B dans le laboratoire était stationnaire et notait que la vitesse de la lumière devrait être d'environ C dans les deux directions. Développons maintenant notre interféromètre pour englober la terre. Nous déplaçons notre observateur B vers le pôle Nord, où il plane, ne tourne pas, et notre observateur A est placé dans le laboratoire à la surface de la terre, avec notre source et notre détecteur. Notre chemin de lumière circulaire est maintenant l'équateur de la terre. Cette configuration est en fait l'expérience proposée par Albert Michelson en 1904. [6] Puisque la source, le détecteur et l'observateur A sont tous sur la surface de la terre, de leur point de vue, ils sont stationnaires (à l'exclusion de la connaissance préalable). Cependant, comme précédemment, A observe la vitesse de la lumière atteignant le détecteur après avoir parcouru le globe pour être respectivement C + v et C - v pour les trajets de lumière bleue et rouge, où v est la vitesse de rotation de la Terre sur son axe (465 Mme). De plus, l'observateur B au pôle Nord peut voir la Terre tourner sous lui, donc de son point de vue, les chemins sont encore inégaux et la vitesse de la lumière est à peu près constante de sa perspective.

Donc maintenant nous pouvons voir que le cadre de laboratoire n'est pas une perspective unique - dans le cas où la vitesse de la lumière était approximativement constante dans la trame du laboratoire, dans le cas 2, elle est variable. Cependant, même dans le cas 1, le soi-disant "observateur stationnaire" dans le laboratoire sera capable de détecter la rotation lente de l'anneau beaucoup plus petit de laboratoire en raison de la rotation de la terre sur son axe, jusqu'à 15 degrés par heure, donc la vitesse de la lumière mesurée par cet observateur ne sera pas non plus constante, mais différera par la quantité beaucoup plus petite C +/- (r * W) où r est le rayon de la boucle et W est la vitesse angulaire de rotation de l'observateur latitude.

Cependant, le pôle Nord pourrait être interprété comme une perspective à peu près stationnaire pour les cas 1 et 2. La vitesse de la lumière est-elle toujours constante par rapport à la Terre non rotative (le cadre ECI utilisé dans le GPS)? Encore une fois, nous pouvons montrer que cela n'est pas vrai.

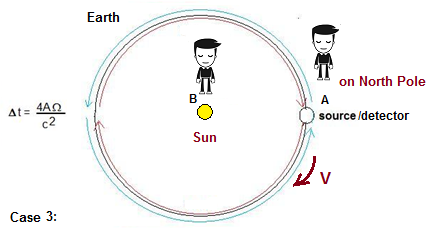
Si l'on considère un troisième scénario (cas 3), où B est sur le Soleil et A sur le pôle Nord, et où les trajectoires lumineuses tournent autour de l'orbite de la Terre, on constate que la perspective du pôle Nord voit maintenant une vitesse variable pour C (+/- la vitesse orbitale de la Terre qui est ~ 30 km / s) et seul l'observateur sur le Soleil voit un C approximativement constant basé sur son observation que les deux faisceaux lumineux ont suivi des chemins plus longs ou plus courts. Mais en utilisant le même raisonnement que dans le cas 2, l'observateur B sur le soleil ne mesurera pas exactement C non plus, mais C +/- une valeur beaucoup plus petite, étant encore C +/- (r * W) où r est le rayon de la galaxie à notre soleil et W est la vitesse angulaire de notre soleil autour de la galaxie.

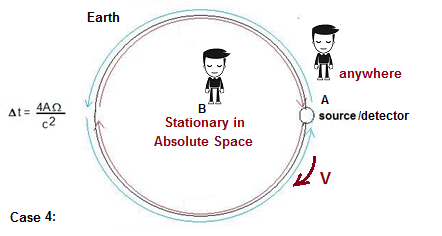
Cette ligne de raisonnement peut continuer à s'étendre à des échelles de plus en plus grandes - par exemple, si A est debout sur le Soleil et B est au centre de la galaxie, alors le centre de la galaxie devient la perspective préférée. En fait, la seule façon de définir un observateur pour lequel toutes les circonstances la vitesse de la lumière C est exactement constante dans un chemin circulaire, est de placer l'observateur B stationnaire par rapport à l'univers.

Toute lumière suivant un chemin circulaire par rapport à B sera toujours observée exactement comme C, mais seulement dans cette perspective. Pour tous les autres cadres de vélocité, la vitesse de la lumière peut être variable. En arrivant à cette conclusion, nous avons établi que l'interféromètre de Sagnac implique qu'il ne doit exister qu'un seul cadre de référence unique pour la rotation, et c'est l'univers lui-même - l'espace absolu, a.k.a. "les étoiles fixes". Donc, pour répondre à la question «par rapport à quoi tourne l'interféromètre de Sagnac?», Nous devons répondre «l'espace absolu, les étoiles fixes». Mais, ce faisant, nous sommes contraints de rejeter l'idée de la relativité du mouvement qui est la pierre angulaire de la théorie d'Einstein.

Les relativistes affirment que l'effet Sagnac peut être expliqué en supposant une vitesse de la lumière constante sur le disque en rotation et en tenant compte de la dilatation temporelle de l'observateur en rotation. Ceci utilise une transformation mathématique vers l'arrière de l'observateur stationnaire. Ce traitement mathématique, attribuable à Langevin et répété par exemple par E.J. Post, a été décisivement réfutée par les expériences Dufour et Prunier. Voir l'annexe A pour la discussion complète.

_____________________________________________________________________________________________

GPS et effet Sagnac - Les satellites GPS doivent utiliser des horloges synchronisées avec le cadre inertiel centré sur la Terre (ECI) - c.-à-d. Que leur horloge d'observation satellite coïncide avec l'observateur non rotatif B sur le pôle Nord du cas 2. Si elles utilisent des horloges synchronisées observateur A à la surface de la Terre dans le cadre fixe de Terre (ECEF) du cas 2 puis la vitesse de la lumière entre le satellite et la terre n'est plus mesurée à C, introduisant une erreur de propagation et donc une erreur dans les récepteurs estimés position. Cette procédure a été utilisée dans la pratique maintenant depuis des décennies.

______________________________________________________________________________________________________________________

La non-relativité du temps

    L'effet Sagnac fait aussi pour le temps ce qu'il fait pour la lumière. Beaucoup d'entre nous connaissent le fameux paradoxe des jumeaux d'Einstein, où un célibataire reste sur terre tandis que l'autre voyage dans une fusée à une vitesse proche de la lumière, revenant des années plus tard pour rencontrer son jumeau. Quand ils se rencontrent à nouveau, le jumeau voyagé est plus jeune que le jumeau de rester à la maison, parce que selon Einstein, la grande vitesse du deuxième jumeau signifiait que le temps progressait plus lentement pour lui que le séjour à la maison jumelle.

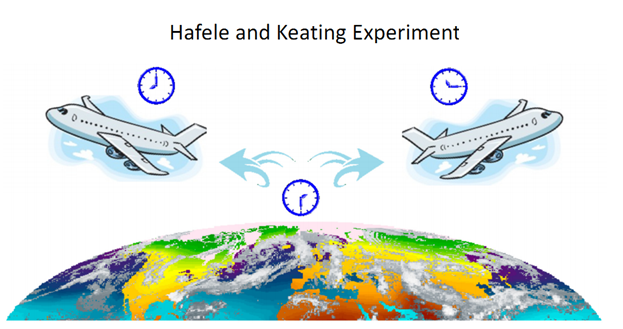
   Cette expérience de pensée a été critiquée par Dingle, [8] qui a fait remarquer que si Einstein soutient qu'une horloge mobile compte plus lentement qu'une horloge stationnaire, mais présume également que tout mouvement est relatif, alors nous devrions pouvoir argumenter avec la même justification que c'est le jumeau lié à la terre qui s'est éloigné à la vitesse du jumeau lié par fusée, et que l'horloge du premier a compté plus lentement à la place.

   Une tentative de résoudre ce problème a été l'expérience Hafele et Keating. Hafele et Keating [9, 10] ont effectué une expérience en 1971 pour tester les prédictions d'Einstein concernant la dilatation du temps dans les horloges déplacées à une certaine vitesse par rapport à une horloge stationnaire. Dans la déclaration d'ouverture du premier de deux articles sur le sujet, les auteurs se réfèrent au débat entourant le «paradoxe des jumeaux» et comment une expérience avec des horloges macroscopiques pourrait fournir une résolution empirique. Dans l'expérience de Hafele et Keating, ils ont piloté des horloges de césium autour du monde dans des directions opposées près de l'équateur, puis ont mesuré combien de temps ils ont gagné ou perdu en revenant au point de départ par rapport à une horloge stationnaire au césium. synchronisé. L'expérience de Hafele et Keating (HK) diffère en réalité du paradoxe des jumeaux - d'abord, dans le paradoxe, le jumeau itinérant se déplace en ligne droite vers un point éloigné puis tourne et revient avec une série d'accélérations et décélérations. Dans l'expérience HK, le voyage est circulaire et les horloges ne quittent jamais l'influence de la Terre. En suivant une trajectoire circulaire, l'expérience HK devient une expérience à effet Sagnac où ce sont des horloges qui bougent plutôt que des faisceaux de lumière.

  Du point de vue de l'observateur au sol, les horloges mobiles de Hafele et de Keating ont connu des mouvements similaires par rapport à l'horloge liée à la terre stationnaire. Si leurs mouvements étaient vraiment «relatifs», alors, selon les règles de SR, ils devraient tous deux revenir au point de départ après avoir subi le même temps de dilatation dans le même sens. Le résultat réel a été que l'horloge à un tour a augmenté dans son taux de temps et l'autre a diminué. C'est le résultat identique à ce que l'on pourrait attendre de la lumière dans l'expérience Sagnac Cas 2, où un faisceau se déplace plus vite que prévu, et l'autre plus lentement que prévu. Et comme précédemment, cela implique que le seul observateur qui voit toutes les horloges compter à un taux proportionnel à leur vitesse est l'observateur au pôle Nord, qui est dans le cadre non-rotatif, géocentrique (ECI) de la terre.

   Comme Murray l'a souligné, Hafele et Keating ont interprété leur résultat en suivant une forme révisée de relativité attribuable à Builder, qu'ils citent dans leur premier article en 1971. Dans "Ether and Relativity" de Builder, il résume comme suit [12]:

     «Le retard relatif des horloges, prédit par la théorie restreinte de la relativité, exige que nous reconnaissions la signification causale des vitesses absolues, ce que supposent aussi les équations relativistes de l'électrodynamique et même la formulation de la théorie restreinte elle-même. les effets des accélérations absolues et des vitesses absolues doivent être attribués à l'interaction des corps et des systèmes physiques avec un certain système inertiel absolu.Nous n'avons pas d'autre alternative que d'identifier ce système absolu avec l'univers.Dans le contexte de la physique, le mouvement absolu doit être compris pour signifier le mouvement relatif à l'univers, toute interprétation plus large ou plus abstraite de l '«absolu» doit être niée Les interactions des corps et des systèmes physiques avec l'univers ne peuvent pas être décrites en termes d'hypothèse de Mach, puisque cela est intenable. pas d'alternative à l'hypothèse de l'éther. "

    La conclusion du constructeur selon laquelle il doit y avoir un "système inertiel absolu" réintroduit le cadre préféré de Lorentz dans la relativité, la chose même qu'Einstein cherchait à éliminer.

   Si nous acceptons l'hypothèse du Builder d'un cadre universel préféré pour le mouvement (éther), alors nous sommes obligés d'accepter l'autre principe critique de Lorentz sur Einstein, que c'est la vitesse de la lumière, et non le temps, qui est la variable fondamentale. dans notre univers. En acceptant une notion de mouvement absolu, ou un cadre préféré, nous sommes comme Dingle, en rejetant la notion de «mouvement relatif». Bien qu'Einstein emprunte beaucoup aux équations et à la théorie de Lorentz et que les deux théories prédisent des résultats similaires pour les mêmes expériences, les deux théories sont philosophiquement antithétiques - et les conclusions sur la nature de l'espace et du temps aboutissent à des modèles entièrement différents. univers.

    Regardons les implications de l'expérience Hafele et Keating sur la relativité du temps. Semblable à notre cas d'origine 3, nous étendons l'expérience de l'horloge itinérante à l'orbite terrestre. Plutôt que des avions, nous plaçons des horloges au césium sur deux fusées et les faisons décoller de la surface de la terre à des vitesses d'évasion égales (disons 12 km / s), mais tournées dans des directions opposées autour du soleil avant de retourner à la terre, comme dans la figure ci-dessous. Les fusées conservent la même vitesse par rapport à la surface de la terre tout au long de leur voyage. Les deux fusées reviennent sur terre à peu près au même moment, et à la même vitesse par rapport à la terre, à 12 km / s. Comme prévu, la fusée à gauche dans le sens inverse des aiguilles d'une montre arrive avec son taux d'horloge ralenti par rapport à l'horloge terrestre, et la fusée à droite dans le sens des aiguilles d'une montre a accéléré son rythme d'horloge, même si leur la vitesse par rapport à l'horloge de surface de la terre était la même. Du point de vue de la terre (en supposant qu'il n'y a pas de présomption de rotation), les longueurs de trajectoire de chaque fusée

semblent être les mêmes. Cependant, un observateur B sur le soleil verrait que les fusées devaient voyager à des vitesses différentes par rapport au soleil afin de voyager à la même vitesse par rapport à la terre en orbite. Les chemins qu'ils ont parcourus semblent également avoir des longueurs différentes lorsqu'on les regarde du soleil. Seul l'observateur sur le soleil serait d'accord que le postulat SR qu'une horloge diminue son taux avec la vitesse est trouvé (approximativement) vrai. L'observateur terrestre A voit cela comme faux - pour lui, les horloges ont parcouru des chemins identiques à des vitesses identiques, mais les horloges se sont désynchronisées. Cela invalide la notion que la trame ECI de la Terre est un cadre de référence unique pour la rotation avec laquelle les lois de SR sont vraies.

   Encore une fois, nous pouvons extrapoler cette expérience de pensée au bord de la galaxie, et plus loin à l'univers entier. Pour les horloges tournant autour d'un observateur, la seule perspective unique où finalement tout mouvement de rotation conduira toujours à un ralentissement de la fréquence d'horloge est le cadre stationnaire de l'univers. Dans tout autre cadre de vitesse, il sera toujours possible de créer des horloges en orbite qui semblent s'accélérer en fonction de notre observateur. C'est la même conclusion que précédemment pour la vitesse de la lumière, sauf maintenant appliquée au temps.

   Ces expériences de rotation ont impliqué qu'il y a un espace absolu avec lequel on peut définir une vitesse de référence de la lumière C, et un cadre de référence préféré pour une horloge temporelle pour laquelle toutes les autres horloges mobiles compteront à un rythme plus lent.

   Puisque Einstein a inventé l'idée d'un temps variable pour expliquer la constance de la vitesse de la lumière, ne faut-il pas en déduire que si nous avons montré que la vitesse de la lumière n'est pas toujours constante pour les observateurs mobiles, alors peut-être? temps "qui est constant, et la vitesse de la lumière est variable en fonction de notre mouvement par rapport à l'espace absolu? Puisque les expériences translationnelles montrent toujours une vitesse de lumière mesurée constante, contrairement à l'expérience de Sagnac, la dilatation apparente du temps est peut-être notre seule preuve indirecte que la vitesse de la lumière est changée de façon cachée pendant le mouvement translationnel. Pour le prouver, nous aurions besoin de concevoir une horloge qui ne dépende pas de la vitesse de la lumière dans son principe de comptage, et de voir si cette horloge n'est pas affectée par la dilatation du temps. Encore une fois, nous allons nous tourner vers l'effet Sagnac et la rotation pour concevoir une telle horloge. Mais d'abord, examinons la base de la dilatation du temps dans la théorie d'Einstein.

L'analogie de l'horloge lumineuse

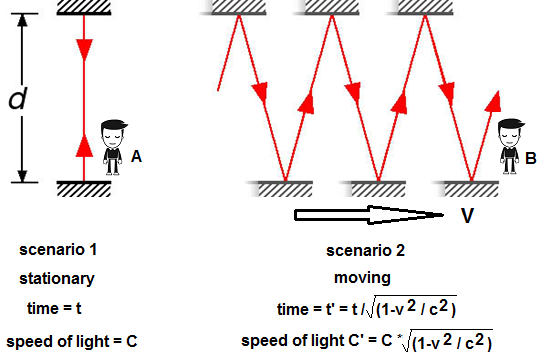
Quand nous voyons une supernova exploser dans le ciel, nous ne disons pas "cet événement vient de se produire", puisque nous savons que la lumière de cet événement a peut-être pris des milliers d'années pour nous atteindre depuis un point éloigné de l'espace. Nous dirions plutôt que l'explosion s'est produite il y a des milliers d'années. C'est parce que notre jugement de la simultanéité des événements est indépendant de la vitesse de la lumière. La vitesse de la lumière pourrait plutôt être utilisée pour insinuer quand un événement aurait pu se produire dans le passé, en fonction du délai de propagation. Alors pourquoi croirions-nous que le temps lui-même dépend de la vitesse de la lumière? Considérons l'analogie d'Einstein, souvent reproduite, d'un faisceau lumineux qui rebondit entre deux miroirs. Dans son analogie, deux miroirs horizontaux se font face et un miroir est espacé de l'autre d'une distance d. Une impulsion lumineuse rebondit verticalement entre les deux miroirs comme indiqué à gauche. Le temps nécessaire à l'impulsion de la lumière pour faire un aller-retour (du miroir supérieur vers le bas et vers l'arrière) est le double de la distance d divisée par la vitesse de la lumière. C'est son horloge lumineuse.

Supposons que «l'horloge lumineuse» se déplace latéralement à une vitesse très élevée (mais constante) de 0,5 ° C. L'impulsion suivrait alors la trajectoire «en dents de scie» indiquée sur le côté droit du dessin. Comme la vitesse de la lumière est la même qu'auparavant (rappelez-vous que la vitesse de la lumière n'est pas modifiée par la vitesse de sa source), il faudra plus de temps pour faire un aller-retour. Donc, notre "horloge lumineuse" prend plus de temps pour compter ses intervalles. Une autre façon de dire cela est que l'horloge "tique" plus lentement.

   Mais voilà le problème. Cette analogie fonctionne parce que la vitesse de la lumière est constante vu par l'observateur A. De son point de vue, il peut voir les deux horloges fonctionner, et bien que la vitesse de la lumière se déplace au même rythme dans le scénario 2, elle a pris un chemin plus long. frapper les miroirs mobiles. En prenant un chemin plus long, il a fallu plus de temps pour atteindre la fin (basé sur l'horloge de A - 1,1546 x plus long ou t / 0,866 = t '). Mais comme nous avons déjà dit que le temps est indépendant de la vitesse de la lumière, nous ne pouvons pas supposer que le temps "réel" est plus lent pour l'observateur B que pour l'observateur A, nous pouvons seulement conclure que l'horloge de B est mécaniquement plus lente. Il a fallu plus de temps à la lumière pour parcourir la distance entre les miroirs du scénario 2. Maintenant, si l'observateur B mesure la vitesse de la lumière dans son image en temps réel, c'est-à-dire une horloge non affectée par la vitesse de la lumière, il devrait conclure que la vitesse de la lumière est inférieure à C, '. C'est exactement comme la situation de l'interféromètre de Sagnac - l'observateur B ne sait pas qu'il bouge, donc il perçoit les miroirs l'un en face de l'autre et séparés par la distance d, il mesure donc la vitesse de la lumière à moins de C. Il ne sait pas que du point de vue de l'observateur A, le chemin d s'est allongé. Alors pourquoi conclut-il que la vitesse de la lumière est plutôt C? C'est parce qu'il mesure le temps écoulé en utilisant une horloge qui est basée sur le temps qu'il faut pour que la lumière passe entre ses propres miroirs mobiles. En effet, son horloge mobile est calibrée par la vitesse de la lumière vue dans son propre cadre (qui est de 0,866 * C), donc par conséquent, son horloge compte plus lentement d'exactement cette quantité (t / 0,866). Cela lui fait faussement mesurer que le faisceau lumineux est arrivé à la vitesse C au lieu de C * 0,866.

    Si la vitesse de la lumière était réellement C dans son cadre, c'est-à-dire C = C ', alors son horloge lumineuse serait plus rapide (maintenant t = t') alors qu'il mesurerait encore la vitesse de la lumière C avec son horloge, la différence de temps entre A et B disparaitrait! Comme le ralentissement des horloges (dilatation apparente du temps) se produit dans la réalité, cela implique, comme dans l'expérience de Sagnac, que la vitesse de la lumière n'est en réalité que C dans le cadre stationnaire, et dans le cadre mobile elle est effectivement , mais est mesurée à tort comme étant C dans son cadre en raison de l'erreur de ralentissement introduite dans son horloge mobile par le plus long trajet de la lumière.

     Nous pouvons aller plus loin - l'analogie de l'horloge lumineuse explique pourquoi chaque expérience de translation pour mesurer la vitesse de la lumière montre que la vitesse de la lumière est toujours C - car les horloges utilisées pour mesurer C sont calibrées à la vitesse de la lumière ce facteur de correction intégré ajuste toujours la vitesse mesurée à C. Cependant, dans chaque expérience de rotation, il est trivial de mesurer une vitesse de la lumière qui n'est pas C. C'est parce que, comme nous l'avons montré avec Hafale et Keating, dans les trajectoires de rotation autour d'un disque ou d'une sphère vont se désynchroniser - en utilisant une origine commune comme référence et un chemin circulaire vers le détecteur confond la capacité d'auto-correction d'une horloge lumineuse, et la différence sous-jacente de la vitesse la lumière par rapport à l'origine est révélée.

L'horloge de Sagnac:

    Comme nous l'avons dit précédemment, pour prouver que la dilatation temporelle est une illusion, il faudrait concevoir une horloge qui ne dépende pas de la vitesse de la lumière dans son principe de comptage, et voir si cette horloge n'est pas affectée par la dilatation temporelle. Encore une fois, nous nous tournons vers la caractéristique essentielle de l'effet Sagnac, la rotation, pour concevoir une telle horloge. Ce concept a d'abord été proposé dans notre article "Le paradoxe des horloges aux Canaries" en 2010.

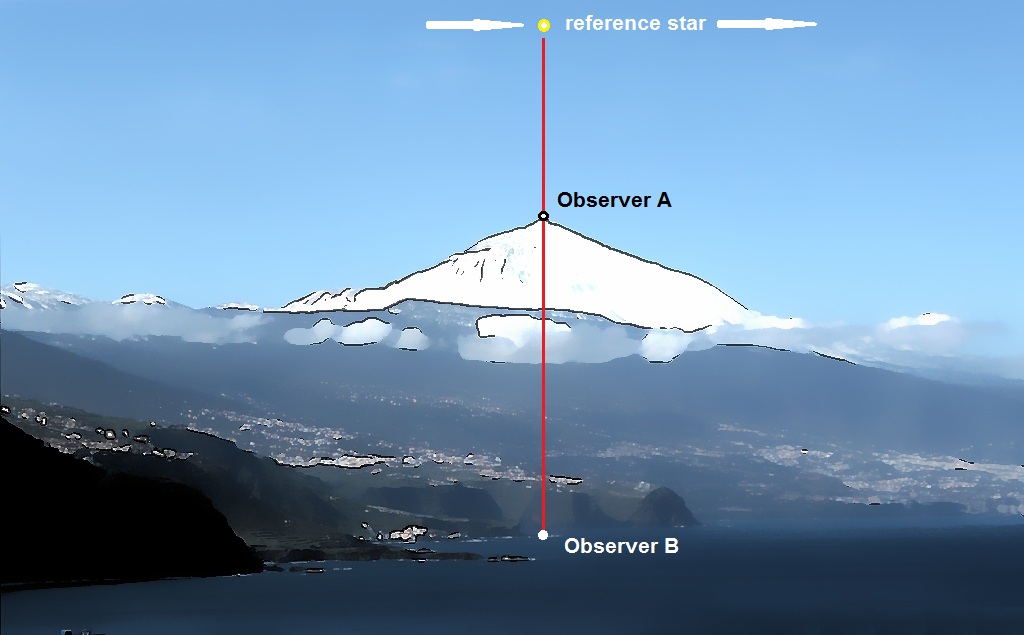
    L'effet de dilatation du temps le plus simple à tester est la dilatation temporelle gravitationnelle, l'accélération des horloges avec l'altitude. Selon Einstein, la vitesse du temps suit le potentiel gravitationnel, de sorte qu'une horloge à la surface de la Terre devrait compter plus lentement qu'une horloge à haute altitude, comme au sommet d'une montagne. On dit que le temps avance dans le futur plus vite au sommet d'une montagne. Nous avons donc besoin d'une horloge sur la Terre qui ne soit pas affectée par l'altitude. Disons que nous utilisons la rotation de la terre comme notre horloge au lieu d'une horloge conventionnelle au césium. Après tout, notre concept humain du temps, et les unités qui le composent (jours, heures, minutes, secondes) sont déjà dérivés de la période de rotation de la terre, donc ce devrait être l'horloge idéale pour la comparaison. Pour chaque observateur, nous pourrions utiliser comme référence la position du soleil dans le ciel, ou la position d'un pendule de Foucault, ou de préférence la position des étoiles fixes en temps sidéral. Si nous mesurons le jour sidéral (23,93447 heures) comme temps de rotation terrestre par rapport à l'équinoxe vernal, en utilisant une étoile de visée comme référence, nous pouvons placer un observateur A au sommet d'une montagne, et un autre observateur B à niveau de la mer. De préférence, l'observateur de la montagne est exactement vertical par rapport à l'observateur du niveau de la mer, et cette ligne verticale traverse le centre de la terre, comme le montre l'image ci-dessous. Nous utilisons comme exemple la montagne Pico del Teide à Tenerife, avec une altitude de 3718 mètres. Nous donnons à chaque observateur A et B une horloge au césium et une horloge sidérale. Les horloges sidérales marquent une coche lorsque l'étoile de référence est directement au-dessus de la tête chaque jour. Les horloges au césium marquent une coche lorsque 23,93477 heures se sont écoulées dans leur heure locale. Nous comparons ensuite les quatre horloges pour déterminer si elles comptent au même rythme.

   Ce qui se passe est que lorsque l'étoile de référence passe sur la ligne verticale rouge passant par l'observateur A et B, les deux horloges sidérales n'ont d'autre choix que de se déclencher au même moment, ne différant que par le temps de propagation de la lumière entre A et B. le temps est un montant fixe, il n'affecte pas la vitesse à laquelle les deux horloges comptent - donc le taux de comptage est exactement le même. Cependant, comme les deux horloges au césium subissent une dilatation gravitationnelle, l'horloge au césium de l'observateur A doit compter plus vite que l'horloge au césium de l'observateur B. Si nous avions pré-synchronisé les deux horloges au niveau de la mer, l'horloge sortir de la synchronisation avec

les trois autres horloges, et le temps gagné par l'horloge de césium A continuera à augmenter au fil des jours. Il est clair que trois des quatre horloges s'accordent sur le temps écoulé - seule l'horloge de césium A se lit par erreur. Le fait que nous ayons créé des horloges immunisées contre la dilatation du temps implique que le temps réel n'a jamais changé au sommet de la montagne - la dilatation du temps apparent est un artefact de la différence de vitesse de la lumière à deux points de différence dans l'espace. horloges calibrées à la vitesse de la lumière - c'est à dire les horloges légères d'Einstein.

Cette conclusion est également cohérente avec notre raison - étant donné les millions d'années que la montagne a été autour, le sommet de Pico del Teide devrait maintenant être plusieurs minutes dans le futur par rapport à la terre à sa base de la mer. Et pourtant, ils sont physiquement connectés. Croire que la dilatation du temps est réelle nous obligerait à supposer que marcher dans la montagne équivaut à marcher dans le futur - la terre devrait former un pont entre deux points de la dimension temporelle d'Einstein. Il est un peu trivial de voyager au sommet de la montagne et de voir à travers un télescope une tour de l'horloge à Puerto de la Cruz loin ci-dessous pour vérifier que le sommet de la montagne et la station balnéaire partagent le même cadeau.

L'auteur au sommet du Pico del Teide en 2012, en vérifiant l'heure. Puerto de la Cruz est clairement visible 3718 mètres plus bas. Toujours dans le présent ...

Conclusions:

On fait souvent valoir que les prédictions de la relativité restreinte et générale ont été continuellement vérifiées et que, par conséquent, la théorie est incontestable. Cependant, d'autres théories, telles que les théories de l'éther de Lorentz modifiées pour tenir compte des effets gravitationnels, peuvent également faire des affirmations similaires. Il existe en effet de multiples voies mathématiques permettant de parvenir à une prédiction correcte, mais ces théories peuvent impliquer des interprétations très différentes de ce qu'est notre réalité physique. Et ceci est au cœur de ce qui ne va pas avec la théorie de la relativité - il peut faire des prédictions réussies basées sur les mathématiques, mais implique une nature du temps et de l'espace non seulement incompatible avec la logique et la raison, mais même contradictoires. Notre interprétation est que ces problèmes surgissent à cause du passage du temps absolu / vitesse variable de la lumière de Lorentz (1904) [13] au temps relatif / vitesse absolue de la lumière d'Einstein (1905) - deux positions qui sont seulement légèrement différentes mathématiquement . En faveur de Lorentz, l'effet Sagnac démontre qu'en fonction du placement de l'observateur, il est possible de voir cette vitesse variable de la lumière et de confondre la dilatation apparente du temps. Notre analyse de l'horloge lumineuse d'Einstein a montré qu'il comptera toujours dans l'erreur si la vitesse de la lumière n'est pas C dans le cadre mobile. De plus, notre expérience de pensée avec les horloges sidérales a montré que la prémisse entière que la dilatation du temps correspond à un changement de temps «réel» est très discutable. Donc quand on réfute avec l'argument que la relativité générale peut expliquer l'effet Sagnac, on peut se demander, pourquoi s'embêter? Si la dilatation du temps est une illusion, alors tout le continuum temps-espace 4D d'Einstein devrait être considéré, pour utiliser son propre mot pour l'éther, «superflu». [7]

References:

[1] Moon, Parry, Spencer, Domina Eberle, and Uma, Shama, (1991) The Sagnac Effect and the Postulates on the Velocity of Light.

[2] Ruyong Wang (2003) Modifed Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber.

[3] Alexandre Dufour, Fernand Prunier (1942) On the Fringe Movement Registered on a Platform in Uniform Motion

[4] Georges Sagnac (1913) Regarding the Proof for the Existence of a Luminiferous Ether using a Rotating Interferometer Experiment.

[5] Rizzi, Guido, (2003) The Relativistic Sagnac Effect: two derivations.

[6] A. Michelson, (1904) "Relative Motion of Earth and Aether." Philosophical Magazine (6), 8, 716-719.

[7] Albert Einstein (1905) On the Electrodynamics of Moving Bodies.

[8] Herbert Dingle (1980) The Twins Paradox of Relativity.

[9] Hafele, Joseph C.; Keating, Richard E. (July 14, 1972). "Around-the-World Atomic Clocks: Predicted Relativistic Time Gains". Science 177 (4044): 166–168. Bibcode 1972Sci...177..166H. doi:10.1126/science.177.4044.166. PMID 17779917.

[10] Hafele, Joseph C.; Keating, Richard E. (July 14, 1972). "Around-the-World Atomic Clocks: Observed Relativistic Time Gains". Science 177 (4044): 168–170. Bibcode 1972Sci...177..168H. doi:10.1126/science.177.4044.168. PMID 17779918.

[11] Murray, W.A. Scott, "If you want to know the time..." Wireless World. 92 No.16 28-31 1986.

[12] Geoffrey Builder (1957) Ether and Relativity.

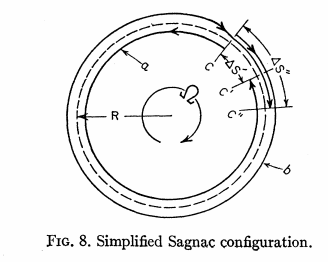
[13] Hendrick Lorentz (1904) Electromagnetic phenomena in a system moving with any velocity smaller than that of light.

Annexe A

Explication cinématique de Post sur l'effet Sagnac:

E.J. Post [19] utilise la position d'observateur stationnaire où la vitesse de la lumière est supposée être c, puis travaille en arrière pour essayer de montrer que le résultat mesuré de l'observateur mobile est le même. Du point de vue de l'observateur stationnaire:

Position C = origine / détecteur

Ds '= la distance C a tourné dans le sens des aiguilles d'une montre au moment où le faisceau dans le sens inverse des aiguilles d'une montre l'atteint en C'

Ds "= la distance C a tourné au moment où le faisceau dans le sens horaire l'atteint en C"

c = vitesse de l'espace libre de la lumière.

Différence de temps pour chaque trajectoire t '= sens anti-horaire, t "= sens horaire

Du point de vue de l'observateur stationnaire, la différence de temps est alors:

L'intervalle de temps du séparateur de faisceau tournant est alors calculé comme suit:

Où g correspond au facteur de dilatation temporelle dû au mouvement de rotation. Cependant, la correction relativiste à l'équation de Sagnac fait-elle réellement une différence dans le résultat réel? Lorsque nous considérons l'interféromètre rotatif de Sagnac comme un dispositif qui subit une dilatation temporelle, nous devons d'abord considérer quelles parties sont des horloges et ce que la dilatation du temps réel aura sur le système de mesure, le détecteur. Regardons l'interféromètre de Sagnac en trois parties:

a) Une source telle qu'un laser, qui est une horloge lumineuse soumise à une dilatation temporelle de la vitesse

b) Un chemin optique composé de longueurs d'onde de la lumière émise

c) Un détecteur qui mesure la différence de phase entre les fronts d'onde des deux faisceaux de retour.

La source (par exemple un laser) est une vraie horloge - laisse supposer que cette horloge éprouve une dilatation du temps proportionnelle à

t’ = t_o/SQRT(1-WR^2/c^2) = t_o * b . puis,

Dt = t_o * b - t_{o =}(2L- 2L/b)/C (1)

Cela signifiera inévitablement que la source en rotation doit émettre de la lumière à une fréquence réduite, proportionnelle à f '= f * SQRT (1-WR ^ 2 / c ^ 2). Cependant, puisque C = f * l, les longueurs d'onde dans le chemin optique doivent augmenter en raison de la fréquence plus basse. Cela signifie qu'il y aura moins de longueurs d'onde passant le détecteur par unité de temps. La différence sera dans le temps qu'un front d'onde donné est derrière par rapport à la situation laser non affectée:

Dt = (2L- 2L/b)/C (2)

Donc, les fronts d'onde sont en retard de la quantité Dt. Mais comme nous l'avons montré en 1, le temps est également en retard de la même quantité Dt puisque la durée de chaque seconde est plus grande en raison du changement de fréquence d'horloge. Le résultat est que les deux effets s'annulent, et le même front d'onde arrive au détecteur au même temps écoulé quelle que soit la dilatation du temps, du point de vue de l'observateur sur le disque. La correction relativiste semblerait ainsi inutile. Comme le dit Post, le résultat est trop petit pour être distingué expérimentalement, et la pratique courante consiste à utiliser un facteur g = 1.

Cela ne contredit donc pas la notion que la vitesse de la lumière mesurée par un observateur sur le disque est C +/- WR.

Post dit lui-même que "les temps de circulation t1 'et t2' dans le cadre tournant sont obtenus en intégrant f 'de 0-2pi et 0 -2pi, respectivement:

Et puis il est facile de voir que dans le cadre tournant:

Dt = L/(C+WR) – L/(C- WR) = 4AW/c^2 (3)

Post cite la méthode de Langevin dans ses articles de 1921 et 1937. Dans son article de 1921, Langevin affirmait que parce que l'effet Sagnac était de premier ordre, il ne pouvait y avoir aucune distinction entre les dérivations newtoniennes ou relativistes et, par conséquent, l'effet était en accord avec la théorie de la relativité. Dufour et Prunier prirent Langevin à l'ordre. Le travail de Dufour et Prunier est discuté par Kelly [17] dans son livre "Challenging Modern Physics: Interroger les théories de la relativité d'Einstein". Dans leurs expériences, ils ont créé des interféromètres Sagnac qui étaient des composites de trajectoires mobiles et stationnaires, y compris des sources fixes et des détecteurs stationnaires. C'était essentiellement pour tester si l'approche relativiste pouvait être distinguée de l'approche classique. En particulier, ils se sont concentrés sur le traitement mathématique de Langevin, par lequel le placement de la position de l'observateur sur le disque est arbitraire. En utilisant le calcul de Langevin:

Dt = L/C + 2WA/C^2 (4)

Ils ont prédit que dans un interféromètre de Sagnac où seulement une partie du trajet de la lumière tournait et l'autre partie stationnaire, l'équation classique demanderait une aire A différente de l'équation relativiste pour calculer le résultat. Dans tous les cas de ce test expérimental, l'effet Sagnac était le même. Cela a renversé l'analyse de Langevin, et en 1937, [14] il a dû réviser son explication, comme l'a souligné Kelly:

Dans son dernier essai sur le sujet en 1937, Langevin propose que les résultats publiés cette année par Dufour et Prunier montrent qu'il faut supposer soit que (a) la vitesse de la lumière varie à c + wr dans un sens et c - wr dans le dans l'autre sens, ou (b) le temps à bord de l'appareil à filer devait varier d'un facteur de +/- 2wA / c2 dans les deux sens. En effet, Langevin est allé jusqu'à dire qu'en supposant (a), «on trouve, par un raisonnement très simple et très général, la formule de la différence des temps du trajet des deux faisceaux lumineux dans l'expérience de Sagnac. Il a également déclaré que «les chemins sont de longueur inégale en raison de l'inégalité de la vitesse de prorogation».

La proposition (b) est cependant indéfendable car si cela était vrai alors quand le faisceau lumineux reviendrait au détecteur en mouvement, l'heure locale de chaque direction serait désynchronisée, ce qui signifie que les horloges ne peuvent pas compter en temps réel et que le la dilatation du temps n'a pas de sens. C'est ce qu'a également souligné Herbert Ives dans son article de 1938 [16] critiquant Langevin. Ives dit à propos de l'absurdité de la proposition de Langevin (b):

"Il n'y a bien sûr pas seulement deux horloges, mais une infinité d'horloges, où l'on inclut celles qui pourraient être transportées à des vitesses finies, et autour d'autres chemins. Comme souligné précédemment, l'idée de "temps local" est indéfendable, ce que nous avons sont des lectures d'horloge. Un nombre quelconque de lectures d'horloge au même endroit est physiquement possible, en fonction du comportement et de l'historique des horloges utilisées. Plus d'un "temps" à un endroit est une absurdité physique. "

La seule explication qui reste, est la proposition de Langevin a) que la vitesse de la lumière varie de C +/- wr dans l'une ou l'autre direction autour du disque, en accord avec les résultats expérimentaux de Dufour et Prunier.

References:

[14] Paul Langevin – (1937) On the Experiment of Sagnac. Compt. Rend. 205, 51.

[15} Paul Langevin – (1921) Compt. Rend. 173, 831.

[16] Herbert Ives - (1938) Light Signals Sent Around a Closed Path.

[17] Al Kelly, Challenging Modern Physics: Questioning Einstein's Relativity Theories”.

[18] A. Dufour, F. Prunier, On a Fringe Movement Registered on a Platform in Uniform Motion (1942).

[19] E. J. Post, Sagnac Effect, Review of Modern Physics, 39,2,