Explanation of the Physical Lorentz Contraction and Time Dilation

based on Schrodinger’s Physical Model of the Electron

Doug Marett, April, 2022

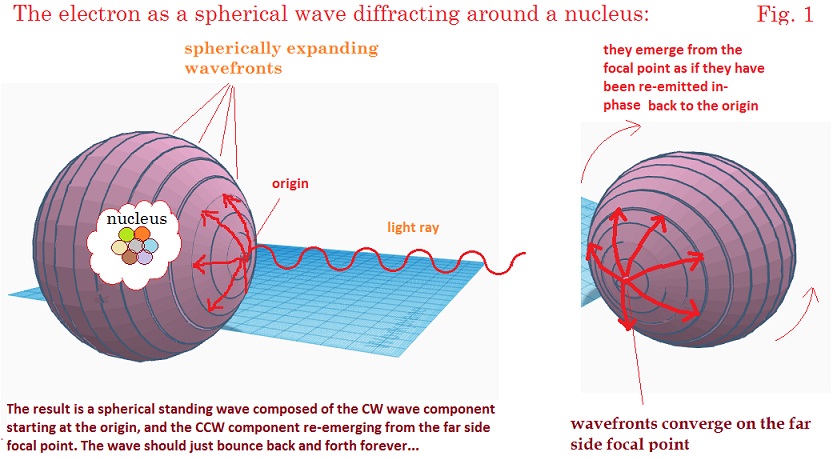
   In Schrodinger’s visual model of the electron first put forward in 1926, and again described in his 1933 Nobel Prize address, the electron was conceived of as a “diffraction halo” around the nucleus. In this model, the EM waves become trapped into a spherical path by diffraction and the wavefronts oscillate between the two polar ends of this sphere, forming an EM shell. This model was addressed in detail in our previous paper. ¹ and can be summarized in the diagram shown below.

   I would like to describe herein how this model of the electron, or particles in general, should contract in their direction of motion consistent with a physical interpretation of the Lorentz contraction. We would also expect a dilation of oscillation period of spherical standing wave. This assumes the electron is moving with respect to the frame of reference in which the EM energy waves, i.e. a preferred frame for the speed of light as called for In Lorentz’s theory or corresponding states.³  

   In Schrodinger’s 1933 model, the electron comprises a spherical standing wave, where the waves travel in the forward and reverse directions between the poles of the sphere. The wavelength of these waves is on the order of the circumference of the sphere, and an integer or half-integer number of waves must fit the circumference for the electron to be stable. We assume that the standing waves are moving at the speed of light C in some medium in which the structure is at rest, which is our preferred frame for the speed of light of these waves, and would have an average wavelength l=C/f.  If the electron then moves at some velocity v from left to right, we would expect that from the perspective of an observer moving with the electron, the propagation time  t’ of the component of the spherical wave moving in the forward direction over a distance L will become longer with respect to its stationary state by the amount:

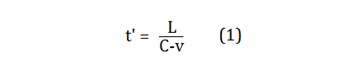
and the wavelength is then shorter by :

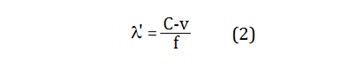
Conversely, the component of the wave moving in the reverse direction will have its propagation time shortened by: 

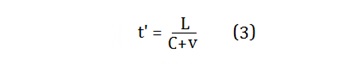
and the wavelength is then longer by:

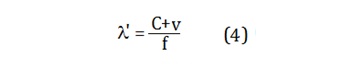
Thereby the average wavelength l’’’ of the standing wave across this segment is the average of the two wavelengths above:

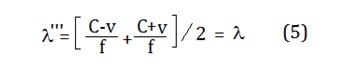
So the average wavelength remains unchanged in the forward/reverse direction. However, for the condition where the EM rays are propagating perpendicular to the velocity v, the propagation time in both directions will be:

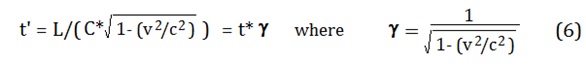
so the average speed of light will be:     C’ = C/ g            (7)

And the average wavelength on the perpendicular segment will be shorter:

l’’’ = l / g                 (8)

For any intermediate segments between the parallel and perpendicular segments, the average two-way wavelength will be shorter, somewhere between l and l/g.

To calculate these intermediate values in an angle-dependent way, we first calculate the one-way wavelength on the segment using the equation below: ⁴

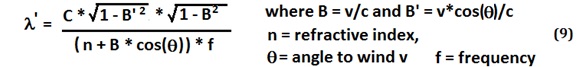
And then use the forward and reverse wavelength at angle q and angle q +180 degrees to calculate the average wavelength l’’’ for the segment.

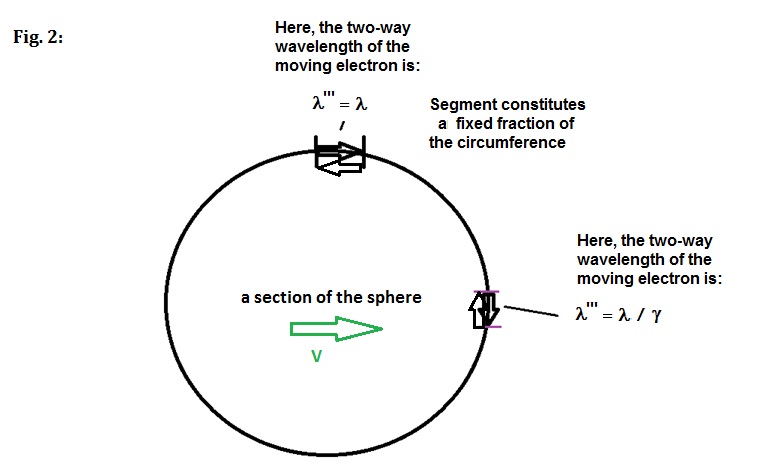
To determine how the sphere would change shape with velocity, we then plot a 2D section of the sphere in Excel as a concatenation of 100 segments covering 3.6 degrees each, and then adjusted these segment lengths as a function of increasing velocity. For the sake of illustration, this circle is 100 integer wavelengths in circumference, each segment being one wavelength.

Each segment is considered to be the average 2-way wavelength in length, since the object we are describing is a spherical standing wave. As the velocity of the shell increases, the local speed of light decreases unevenly around the shell, leading to a shortening of the average two-way wavelengths as one approaches the x-axis. Conversely, the average two-way wavelengths close to the y-axis do not contract since they average to a net zero change in length with velocity. This can be seen in the figure below at various speeds approaching the speed of light:

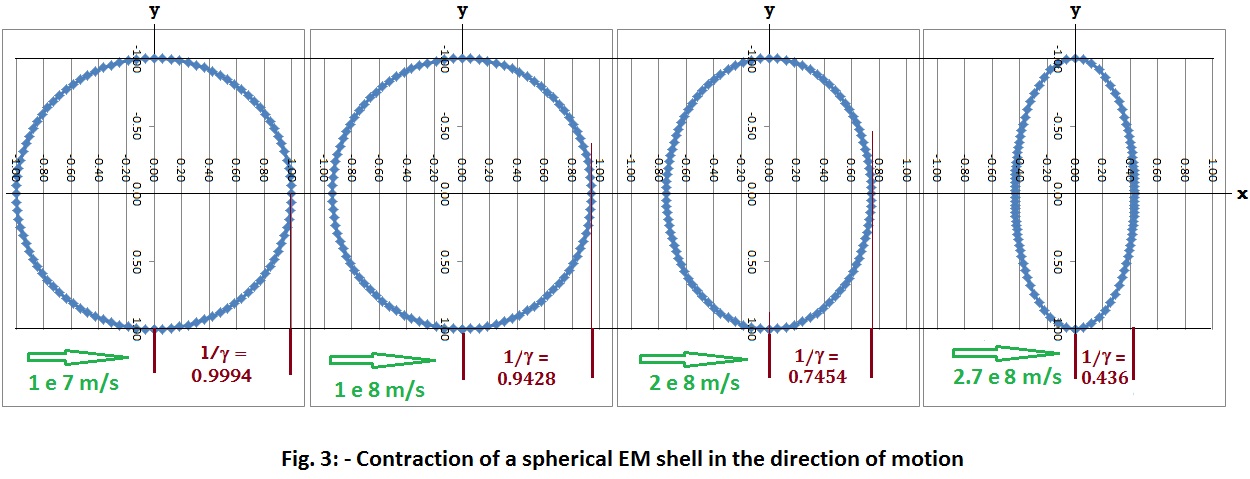
The circumference of the sphere is found to get smaller and smaller with velocity, proportional to SQRT(1-v^2/2c^2), while preserving the total number of concatenated segments at 100. The height of the sphere perpendicular to travel doesn’t change, but the length of the sphere in the direction of motion along the x-axis shortens by SQRT(1-v^2/c^2),  i.e. 1/g,  which is the amount anticipated by the Lorentz contraction. The contraction occurs for a different reason than one might expect – the sections at the front and back of the object close to the x-axis are the ones contracting, and this shortening pulls the ends closer together. This gives us a picture of the proportional change in the shape of the shell with velocity.

The sum of the one-way wavelengths of the EM around 360 degrees of circumference also adds up to a net shortening of SQRT(1-v^2/2c^2), which would be what would be expected if the height remained constant but the width shrinks by the amount of the expected Lorentz contraction.

Explanation of Time Dilation in a Moving Particle:

   If we examine the one-way propagation time of an EM wave across each segment when the shell is moving at velocity V, we find that the propagation time around 360 degrees is now increased. If we take the sum of the one-way propagation time across each contracted segment, based on the calculated speed of light at the given angle for that segment, we find that the beam completes our 100m example circuit in:

3.3333333E-07 seconds,  v = 0 m/s          3.3333358E-07 seconds,  v = 365 km/s

And we find that:      3.3333333E-07 x g = 3.3333358E-07

   So the propagation time has increased by g, and this is after accounting for the circumference shrinking by SQRT(1-v^2/2c^2). If we consider the natural period of the electron to be the oscillation period of the standing wave back and forth across the shell, then this oscillation period t will naturally increase with velocity by the Lorentz factor g. This result has been confirmed experimentally, for example in the Ives-Stillwell experiment of 1938. ² Ives used the transverse Doppler effect to confirm that hydrogen canal rays had their spectral line emissions decrease in frequency with velocity. This follows the relation:

f’= f*SQRT(1-v^2/C^2).

In Ives’s paper, he explains this effect based on the theory of Lorentz – it is not “time” that dilates, but rather, the mechanical oscillation period of the particle.

So in that sense “time dilation” could be considered a misnomer. This result also suggests that there is no need for the electron to loose energy with velocity – the lengthening of the period of these “atomic clocks” is a consequence of the increased time required for the spherical waves to travel around the circumference. The alternative would violate conservation of energy.

This model can all be summarized in the diagram below:

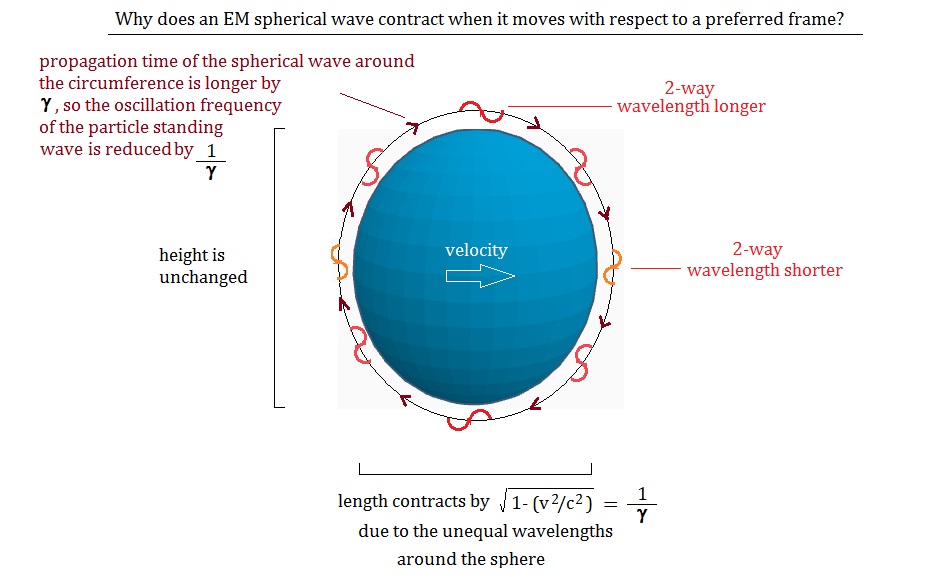
References:

1) Marett, Doug, “Schrodinger’s Wave Model of the Atom – A Physical Interpretation.”  Conspiracyoflight.com website. April, 2022.

2) Ives, Herbert, Stillwell, , G.R., “An Experimental Study of the Rate of a Moving Atomic Clock.” JOSA Vol. 28, No. 7, 1938, P. 215 – 226

3) Lorentz, Hendrick, “The Michelson-Morley Experiment and the Dimensions of Moving Bodies.” Nature, Volume 106, Issue 2677, pp. 793-795

4) See Appendix for more details.

               Appendix – Speed of light calculation in the dielectric light path:

   Calculation of the angle-dependent one-way speed of light on a light path, such as the arm of an interferometer, moving with respect to a preferred frame, has previously been discussed in the work of Lorentz. In 1921 he offered the following equation to express this: ³

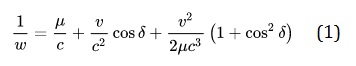
Where w = the speed of light in the arm, u = refraction index, v the velocity with respect to the frame, and c the speed of light in the preferred frame. This equation is somewhat accurate, with small errors in the 0.5 m/s range, but encounters larger errors when n > 1. It also doesn’t include the Lorentz contraction which must be added later to the calculated length of the arm.

To try to overcome these deficiencies, we derived a new equation as follows. If we start from Fresnel drag equation used by Lorentz in similar calculations, we find it can be re-expressed as:

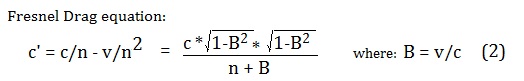
C’ = velocity of light in the arm, v = velocity of the arm with respect to the preferred frame, and n = refractive index of the arm, angle to the wind is 0.

If we now add the Lorentz contraction to the denominator, it cancels out with the equivalent amount in the numerator, leading to the simplified version for the speed of light in a Lorentz contracted arm at angle 0 to the wind.

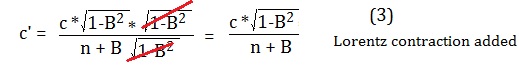
We then correct for the angle to the wind by adjusting the denominator v by the factor cos(q):

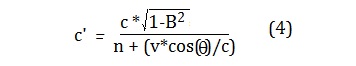
This new equation (4) has been tested in a large number of interferometer simulations and it predicts exactly zero fringe shifts for the motion of interferometers with respect to space as is called for by Lorentz’s theory. This includes for interferometer experiments with RI >=< 1.

The equation used in this paper then corrects equation 4 back to the Lorentz contraction (LC) free version, since the LC is what we are trying to determine in Schrodinger’s moving spherical waves. To get the correct values from 0-360 degrees, an expression shown in red is added to cancel out the angle- dependent LC  that was effectively built-in to equation 4.

From this the wavelength of the concatenated sections of our moving spherical waves can be calculated using C = f * lambda.