Explaining the
Lorentz
Force Using Magnetic Lines of Force. Maxwell’s
Fluid-Mechanical Approach D. Marett (2013) The
Lorentz force is
usually described abstractly without reference to the physical
mechanism by
which the force acts in space. Consider for example and diagram of the
Lorentz
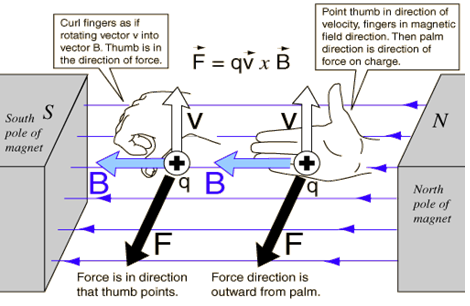
force using the right hand rule, from the website hyperphysics:
1)
The right hand rule:
A
charge moving upwards in the
drawing (in the direction of the thumb) experiences a force outward
from the
palm, when the outstretched fingers point in the direction of the B
field. So
what is the actual physical mechanism
by which the Lorentz force acts? A physical explanation can be hard to
find. We
found one in an old physics textbook by S.G. Starling, Electricity and
Magnetism for Degree Students (7th Ed., 1941) p.
240, reproduced in
Fig. 2:
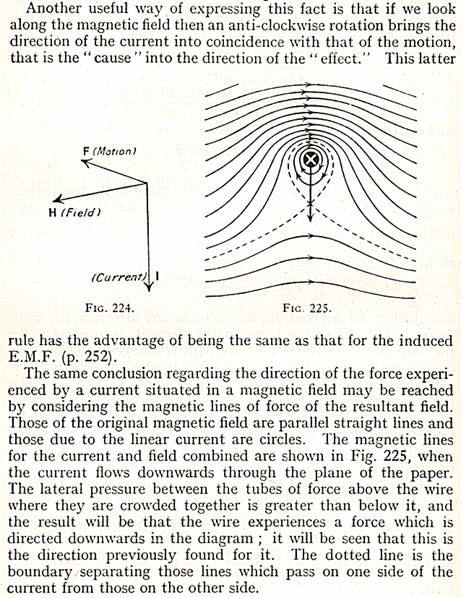
In Starlings, explanation,
magnetic lines are
considered “tubes of force”. He explains that there is a pressure
between these
tubes of force. Note from the diagram that where the B field of the
wire and
the external B field point in opposite directions, there is attraction.
As
Starling says, “an anti-clockwise rotation brings the direction of the
current
into coincidence with that of the motion, that is the “cause” into the
direction
of the “effect.” This premise results directly from fluid mechanics.
The
Lorentz force is derived from James Clerk Maxwell’s equations, and
Maxwell’s
physical model of Faraday’s lines of force were of vortices in a fluid
medium.
They obey Helmholtz’s
theorems of vortex motion. So ultimately, the Maxwellian
physical model of
magnetic lines of force is a fluid dynamic model. Quoting James Clerk
Maxwell
from “On Physical Lines of Force”, P. 455: “Let
us now suppose that the
phenomenon of magnetism depend on the existence of a tension in the
direction
of the lines of force, combined with a hydrostatic pressure; in other
words, a
pressure greater in the equatorial than in the axial direction: the
next
question is, what mechanical explanation can we give of this inequality
of
pressure in a fluid or mobile medium? The explanation which most
readily occurs
to the mind is that the excess of pressure in the equatorial direction
arises
from the centrifugal force of vortices or eddies in the medium having
their
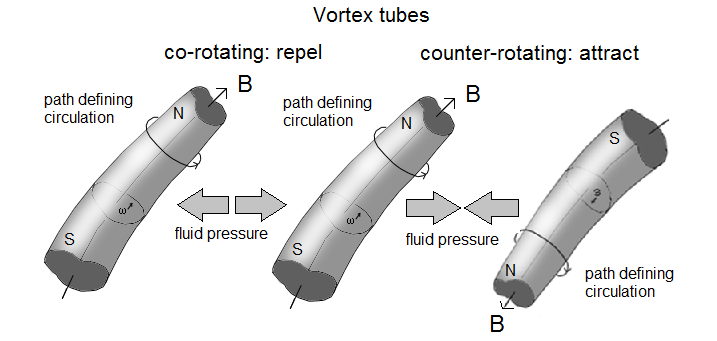
axes in the directions parallel to the lines of force. “ As is known from vortex theory,
counter-rotating vortices attract,
and co-rotating vortices repel. Quoting from Wikipedia:
“Parallel
magnetic lines of force
traveling in the same direction repel one another. Parallel magnetic
lines of
force traveling in opposite directions tend to unite with each other
and form
into single lines traveling in a direction determined by the magnetic
poles
creating the lines of force.” This is shown diagrammatically in Fig. 3
below: Fig.
3:
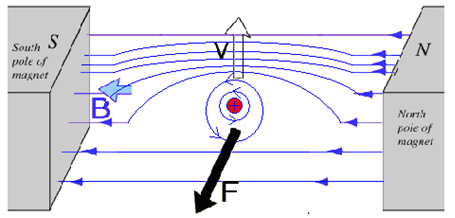
The Lorentz force diagram can now be drawn as shown
below in Fig. 4 to illustrate the phenomenon in terms of the force
exerted by
the magnetic lines. Fig. 4: The Lorentz force visualized as an
interaction
between magnetic tubes.
The
positive charge moving
vertically through the magnetic lines of force generates a magnetic
field
around itself by the right hand rule. The lines of this field are
horizontal,
in the same place as the field lines of the magnet. The lines of the
charge and
the lines of the magnet are co-rotating on the far side, and thus repel
one
another (leading to a pressure on the far side). The lines on the near
side are
counter-rotating, and thus attract one another. As a consequence, the
particle
experiences a force to the near side, with the dark arrow shown. Magnetic
Tubes of Force – real or Imaginary?
With the advent of Einstein’s treatment of
electrodynamics, the magnetic
tube of force has been relegated to an imaginary entity. There may be
some good
reasons to question this modern approach. A
must see video on the subject is Akira Tonamura’s
“Electron
Waves Unveil the
Microcosmos.”(Vega Science Trust). In the video
Dr. Tonamura succeeds in
visualizing bunches of magnetic lines of force
Fig.5:
The late Akira Tonamura
showing a model of a magnetic line bunch (Vega Science Trust).  trapped
in a superconductor, a model of which is shown in Fig. 5. The magnetic
lines of force behave as if they are real structures, moving like
discrete
particles, bumping into obstacles and getting stuck behind walls, etc.
This is
shown vividly in the video, and example of which is shown below in Fig.
6: Fig.
6: Magnetic lines of force
moving as discrete units along a step in a superconductor.
Further,
Akira Tonamura succeeded
in visualizing the annihilation of counter-rotating magnetic vortices.
Vortices
of one orientation were first set up in the superconductor by applying
a strong
magnetic field. Once established, the field was then turned off, and
some
vortices persisted on the surface (often bunched up in cues, waiting to
reach
the edge of the superconductor). Then the opposite magnetic field was
applied,
generating the reverse vortices on the same slab of material. When
these
counter-rotating vortices encounter each other, they annihilate, as
shown below
in Fig. 7. The video shows actual video footage form the electron
microscope of
the process in action. Fig.
7: Counter-rotating magnetic
vortices annihilating on a superconductor surface.
Another
issue arises with the
relativistic approach to magnetic fields. The problem is related to
co-moving
particles. If magnetic field lines were real, then co-moving particles
should
generate magnetic fields around themselves which interact if they are
close
enough to each other, via the Lorentz force. This would be because the
particles would form magnetic fields relative to the medium of space
(after
Maxwell). However, as Einstein would explain it, magnetic fields are
only visible
between particles if there is a velocity difference between them –
co-moving
particles should experience no Lorentz force between them, since the
Lorentz
force would be a function of their velocity difference only. However,
the
phenomenon of Z-pinch
does
arise in co-moving particles, attributed to the Lorentz force, meaning
that
co-moving particles can see and react to each others magnetic fields,
even when
there should be no velocity difference. This could be evidence that
magnetic
field lines are not relative phenomenon after all.
**************** |