Derivation of the "absolute" earth movement
from
observed lengths of Jupiter’s satellites
- Leopold Courvoisier -
Sternwarte
Berlin-Babelsberg, 1930, April 27.
From my previous studies on the movement of
the earth relative to the light aether (s. AN5416, etc.) it can be seen
that
the target point of the general translation movement found is not far
from the
ecliptic (A = 80 deg., D = +40 deg.) and the speed (v = 500km / s) is a
very
substantial one. Accordingly, the maximum difference in light time (t =
v / c)
for appearances on the Jupiter satellites (e.g. eclipses) would be,
like K.F.
Bottlinger noted years ago (AN 5051), principally to determine the
"absolute" solar and Earth movement, respectively, approximately = 7s
(= 2r x v / c)
depending on Jupiter
during the observation geocentrically near the apex or anti-apex of
translation; in the first case the light time was shortened by about
3.5s, in
the second case by just as much. The question now is whether the
accuracy of
the existing satellite observations is sufficient for such a
determination.
After the in-depth discussions that D. Brouwer (1) and W. de Sitter (2)
had on
older and newer observation material, at least an attempt had to be
made from
the outset to evaluate the most homogeneous, modern observation series,
some (A)
of those carried out in Johannesburg Eclipse observations from 1908 to
1926
(and only the entries and exits, arranged by Brouwer and (B) the
photographic records
(arranged by: de Sitter) obtained at the Cape, in Greenwich and Leiden
from
1913 to 1924, appear to be worthwhile in the aforementioned respects
and was
therefore undertaken by me as follows.
A brief overview of the series of annual
averages of the residual values of the observed satellite lengths
given in
the two sources, which remain in comparison with the latest orbital
theory, has
at least consistently identified a pronounced wave in the three inner
satellites, which is of approximately twelve-year period and which, in
terms of
phase and amplitude, also corresponds sufficiently close to the
expected
fluctuation in light time. Since such a phenomenon cannot be
satisfactorily
explained by any of the previously known inequalities in the length of
the
Jupiter satellites, since (according to de Sitter) on the one hand the
period
of the vibration is only about 6 years, but that of the secular
inequalities on
the other hand exceeds 12 years, there is nothing in the way of
actually
viewing it as a periodic change in the time of light caused by the
"absolute" movement of the earth and the solar system, respectively,
the
period of which is Jupiter's orbit.
If one calls aJupiter the respective opposition
right ascension of Jupiter, A the right ascension of the apex of the
"absolute" movement, y the amplitude of the long light-time
fluctuation, expressed in time seconds, respectively, then the latter
in our
case can be reasonably approximated by a sine wave representation,
which
results in the following form of the condition equations:
Rest(s) = x + y cos (aJupiter - A +180 deg)
The adjustments
of the individual remaining series then give values for A and y
respectively,
the speed component in the Jupiter orbit, which can be compared with my
numbers
found elsewhere.
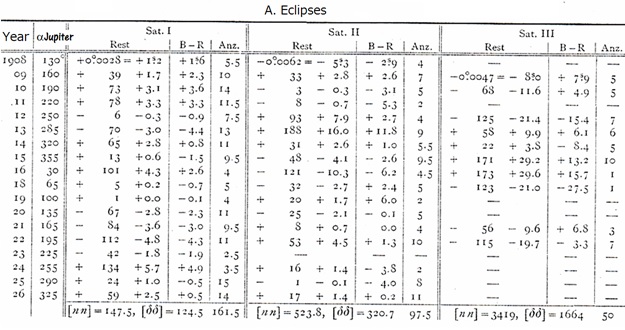
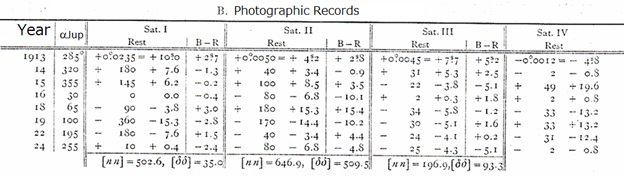
In the tables below, the residual values of
longitude that I have summarized for each observed satellite in annual
mean, as
they emerge from the two observation groups mentioned above, are
expressed both
in longitude degrees and in time, together with their quadrasums (n,
n).
The tables also contain, in addition to the
years of opposition, the approximate opposition right ascension of
Jupiter, the
number of individual observations in the annual averages, and the
residues B-R
of the individual sine waves remaining after my adjustments and their
sums of
squares (dd).
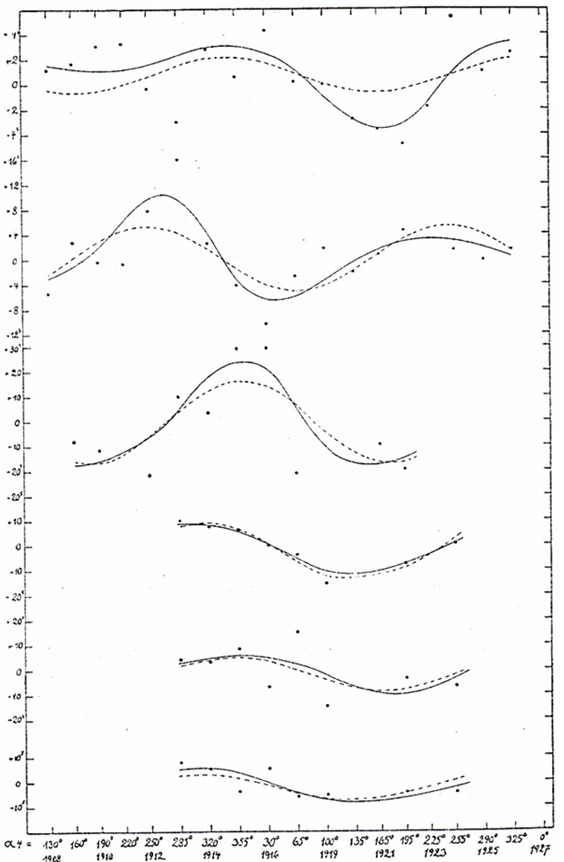
In the figure, these
series of numbers have been shown graphically one after the other for a
more
convenient overview and, experimentally, have also been compensated
graphically
by simple lines. The next tables of the random errors of the
observations
derived from Brouwer and de Sitter provide sufficient information about
the
expected average accuracy of an individual annual or curve point,
respectively.
For comparison purposes, the mean errors of the weight unit resulting
from my
adjustments are also included in these.

When carrying out the
adjustments of the above remaining series for each satellite, the
individual
annual means were given the same weight, since the situation at the
moment can
only be a rough calculation. Furthermore, the adjustment of the
relatively inaccurate
observations of the IV satellite under B., as expected to be useless or
delivering values that are too uncertain, has been completely omitted.
The
adjustments of the six observation series of the three inner satellites
then
give the numerical values compiled below for the unknowns A and y or v
and
their approximated mean errors.

The internal agreement of
these values generally corresponds to the calculated random errors.
With regard
to the error limits, the agreement with the above-mentioned average
results (
A=80 deg., D=+40 deg. V = 500 km/s) that I have received so far is for
the
darkening observations of the I and II and the photographic images of
the II
and III. To call satellites a complete one, for the final mean at least
as good
as can be expected given the circumstances, given the possible
systematic errors
of satellite observations. It must be borne in mind that systematic
errors
occur all the more easily because the observations on average comprise
little
more than one Jupiter orbit. In this regard, it would be very desirable
for the
task dealt with here if these important observations, as well as those
of the
eclipses (Johannesburg) as well as the photographic images of the
satellites,
were to be as homogeneous as possible for at least a second, or at
least over a
second orbit of Jupiter Way could be continued.
L. Couvousier
Sternwarte Berlin-Babelsberg, 1930, April 27.
