The Paradox of the Clocks in the Canaries Doug Marett
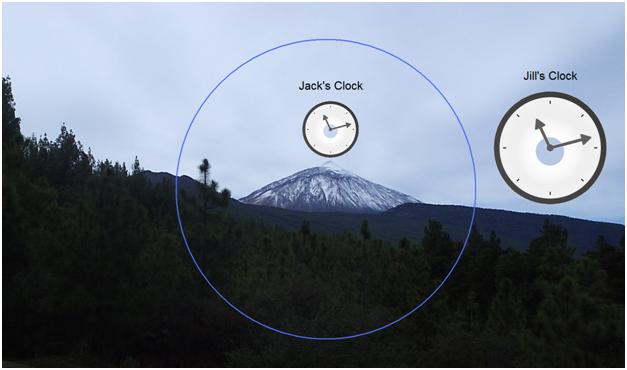
(2010) Einstein's general theory of relativity predicts that the rate of time passage becomes slower as one approaches the center of a massive object such as the earth. Far from the massive body, clocks run faster. He believed this effect is manifested in accelerated reference frames by virtue of the equivalence principle. Does time really pass at different rates at different altitudes? Let us consider a thought experiment to test this idea. Jack and Jill are two fraternal twins living on the island of Tenerife in the Canary Islands of Spain. They both live in the sea-side town of Puerto de la Cruz, from which the peak of Pico del Teide, a mountain of 3718 metres, is visible during fair weather. If Jack were to go up mount Pico del Teide for 10 years, and Jill were to stay at sea level, the clock carried by Jack would advance ahead by 0.13 ms with respect to a clock with Jill at sea level, due to gravitational time dilation. According to this version of the twin paradox, if Jack returns to Jill after 10 years, the moment he arrives at sea level to meet Jill, more time has elapsed (0.13 ms) for Jack and he is thereby older than Jill. However, if Jill goes up the mountain after 10 years, what time does she read on Jack's clock? This question is not straightforward, since we would assume that if time passes faster at the top of the mountain, the mountain clock would be ahead by 0.13 ms, just like when Jack comes down the mountain. However, imagine that Jill view's Jack's clock through a telescope trained to view the top of the mountain, and that it is more or less in constant
Pico del Teide, as viewed from the sea-side town of Puerto de la Cruz.
Close-up of the peak. view from sea level, assuming no cloud cover, as shown in the picture above. If Jill recorded the movement of Jack's clock through the telescope, and had Jill's clock at sea level in the same frame, both events would be viewed as happening in her present. One should think then that the two clocks should progress forward at the same rate, and if time is progressing faster on top of the mountain, then that process is happening in the future of Jill, not the present. Jill should see the two clocks count at the same rate because she views the mountain in her present. To assume otherwise would assume that Jill is viewing the future on the mountaintop, not the present. This then leads to another problem - best shown by adding a third character, Jim. Jim went up the mountain ten years before Jack with a clock. If Jim stands beside Jack at the top of the mountain for the second ten years of his visit, and Jill views both their clocks side by side, she is viewing what she considers to be her present on the top of the mountain. However, after 10 years, Jim's clock is 0.26 ms faster than her clock, and Jack's clock is 0.13 ms faster. The question then becomes - what time is Jill viewing on top of the mountain; is it the present of Jill, or some future time, either Jim's time or Jack's time, which is visible to her in her present? If she sees any time other than her own present through the telescope, then is she viewing into the future? Since Jim and Jack are standing together in the telescope view, Jill views them simultaneously, but from the count on Jim's clock he should be further into the future than Jack. She can't be viewing two adjacent futures simultaneously. Which future does she see? The future of Jim, or Jack, or perhaps a third future, the future of the mountain, which has existed in a different timeframe for eons. We can only conclude that Jim and Jack and the mountain are in substantially the same present as Jill when viewed by Jill, otherwise they could not be viewed simultaneously. Also, if Jill were viewing the future on top of the mountain, the future that she sees would be subject to whomever she is viewing on the mountain. The only rational conclusion is that Jim and Jack have remained in Jill's present all along, even though the visible rates of Jack's and Jim's clocks appear to be different. Any other conclusion would be paradoxical. When we say that Jack and Jill are in the same present, or that two adjacent persons can be viewed simultaneously, we mean that the propagation delay of light, the cause of the relativity of simultaneity, is insignificant compared to the observed time dilation on their clocks. In our examples the distances between observers are short (say a few Km) but the duration of stay of the observers at different altitudes is long (several years). Thus the differences in time observed on clocks are due to accumulated time dilation, and not errors of simultaneity caused by propagation delays of light. This suggests a rule: that if an observer can see an event, then that event must be happening in their present, minus the propagation delay for the light to reach the observer. An observer can't observe an event happening in a different time other than that due to the loss of time from the propagation delay, even if relativity claims that time is progressing at a substantially different rate at some other visible place in space. However, in that same observer's present, multiple clocks can be viewed to be registering different times. Since these different times are viewed simultaneously by the observer (after propagation delay) these differences in the viewed clock readings cannot be due to differences in real elapsed time at different points in space. This is the root of the paradox - if time really moves faster or slower due to the effects of gravity at different altitudes, then observer's at different altitudes should not be able to detect this change in time, since to see a future or past time they should have to actually move into, or see into, the future or the past. An observer can only witness into the past as far as the time lost in the propagation delay of light. If a clock at one altitude has been observed to count substantially faster or slower than a clock with an observer at a different altitude, then this must be an artefact. The counter-intuitiveness of the entire process is highlighted by the following: the observer whose clock counts slower (sea level) is the one moving into the future faster (arrives in the future with less elapsed time). She is younger than the other observer when they meet again. If a clock actually measures the passage of units of time, how can a clock that counts slower result in the observer being further ahead in time than the reverse? The problem arises from the definition of time - is time really a dimension like space? Let's consider the differences between "time" and "space". Spatial distances are made up of points that exist concurrently. The corners of a block of wood exist in the same "now". Classically however, duration (time) is composed of points (the present) that do not exist concurrently. The present from 5 minutes ago does not co-exist with the present now. The difference between the two is well resolved in the following quote: "...duration is an entirely different notion from "space." Duration is not an "entity" like space. Duration arises when the present persists--when the present endures; and it allows us to speak of earlier and later "nows." Spatial distances, in contrast, do not emerge from a persisting present and do not accommodate the notion of "earlier and later"... duration can also be defined as "a period of elapsed or elapsing time." If we were to characterize the distance between two points, A and B, as "a duration of one year," we would be claiming the following: "The time that elapses when an individual relocates from A to B is precisely one year. One cannot relocate from A to B in an elapsed period that is less than one year. One cannot relocate from A to B in an elapsed period that is greater than one year... The time from the beginning to the end of a duration does not vary. This is true by definition." However, if we consider Einstein's notion of time dilation, it is implied that one can move from A to B in more or less time than 1 year. Einstein treats time as if it is a kind of space, so paths of different lengths in time can bridge A and B. This suggests that the time from the beginning to the end of a duration can vary, contrary to our above definition of time. But what does this really mean? Is it the clocks that speed up or slow down independent of the passage of real time? As is known from the "light clock" analogy, one light clock ticks slower than another because the path of the light in the slower clock is longer. It is not necessarily true that our definition of the duration of time has been violated between A and B. From another point of view, relativity hinges on the idea that each tick of a clock represents the same amount of time, regardless of how fast or slow it is going. If this were not true, then the twin with the faster clock would not be older than the twin with the slower clock. Conversely, from a Lorentzian point of view, the opposite is true - if a clock counts faster or slower, it is faster or slower than some absolute time, to which each clock has incurred an error. This highlights another enigma of the twins paradox - if each clock counts the same duration for each second, and one clock counts more seconds than the other, how do the two twins meet at the same point in the future with their respective clocks? The only conclusion is that either one clock or both no longer counts the same duration for one second. But to accept this conclusion undermines Einstein's argument that one twin is older than the other. Relativity requires that there are two definitions of time, the one "perceived" and the one "static". The contrast between the dynamic (temporal) time and the static (spatial) "time" is that the former is the subjective time of the mind, while the latter is simply the fourth dimension of a unified 4-dimensional structure known as "spacetime." However, the inability to perceive static (spatial) time may be because it does not exist! To quote Erwin Schrodinger: "The world is given to me only once, not one existing and one perceived. Subject and object are only one. The barrier between them cannot be said to have broken down as a result of recent experience in the physical sciences, for this barrier does not exist." The entire premise of space-time is based on the idea that the speed of light C is the same for all inertial observers. Since C = D/T, then D = CT, and if C is a constant, then time can be expressed in units of distance. However, if the constancy of the speed of light is an illusion of the Lorentz transformations, as Lorentz himself believed, then the speed of light is a hidden variable and time cannot be expressed in distance - spacetime would then be a dead theory. What is critical is to prove that the clocks that speed up or slow down in their measurement of time are affected by the hidden variable speed of light. If we could design a clock that is unaffected by the gravitational potential of our two observers, then we might be able to show that this clock counts the true duration, and the others are in error. The Sidereal Time Clock Can we prove that the rate of these clocks do not properly count the real passage of time? By these clocks we refer to the most accurate clock currently available - caesium clocks. We need a clock on the Earth that is unaffected by gravitational altitude. Let's say we use the rotation of the earth as our clock instead of a conventional clock. For each observer, we could use the position of the sun in the sky, or the position of a Foucault pendulum, or most preferably the position of the fixed stars in sidereal time. After all, our human concept of time, and the units that compose it (days, hours, minutes, seconds) are already derived from the rotation period of the earth, so it should be the ideal clock for comparison. If we measure the sidereal day (23.93447 hours) as the time for one earth rotation relative to the vernal equinox, using a sighting star as a reference, the caesium clocks that Jack and Jill carry would disagree on the time elapsed after 10 years, but the sidereal day clocks for Jack and Jill would agree. If the positions of Jack and Jill are fixed on the Earth's surface but differ only in altitude, then they would have to agree (minus the propagation delay of light) on the length of one sidereal day since a star in the sky would pass across the zenith for both of them at the same time. Since it is impossible for Jack and Jill to measure a different sidereal time at different altitudes, we have created an absolute time clock for Jack and Jill, to which the caesium clocks that they hold disagree. This proves that Jill at sea level has not actually moved into the future at a different rate than Jack on the mountain - in fact, absolute time has passed at the same rate for both - the caesium clocks have simply counted at different rates for some other reason. The only plausible explanation is that caesium clocks count faster or slower at different altitudes due to differences in the propagation time for light inside the clocks, not differences in the passage of absolute time. Based on the age of the current peak of Pico del Teide, if Einstein were right the summit should be around 10 minutes in the future compared to its sea level base, despite the fact that they are physically connected. Velocity Time Dilation and the
Sidereal Time Clock. We now address velocity time dilation in the same manner. Let's say that Jack flies with a caesium clock at 1000 meters above sea level at a constant velocity of the earth's rotation speed at the latitude of Pico del Teide, in an easterly direction (409 m/s). Jill sits on the side of the mountain at the same altitude with her caesium clock. Both Jack and Jill have a second clock that is synchronized to sidereal time by the position of a set star. Jack times the start of his journey so that when the set star is at Jill's zenith, it is also at Jack's zenith, once every sidereal day (Jack passes over Jill once per day). Since according to Einstein, Jack will experience a velocity time dilation of v^2/2c^2 with respect to Jill, after 10 years Jack's clock should be slower by 0.88 ms (using the Hafele and Keating method). If Jack lands after 10 years, he should be younger than his twin Jill by this amount, since his caesium clock reads 10 years - 0.88 ms. However, his sidereal clock, which has also been counting this entire time, agrees with Jill's sidereal clock, that exactly 10 earth years have elapsed. We thus have a contradiction. Another problem arises because according to special relativity, one should not be able to determine which observer is moving faster, thus Jill should see Jack's clock as slower, and Jack should see Jill's clock as slower. Since in the actual Hafele and Keating experiment, the clock that is slower depends on which direction Jack travels around the earth (east or west) the reciprocal effect of velocity time dilation fails. If Jack were to fly west instead of east at 409 m/s, his caesium clock would actually count faster than Jill's. The caesium clocks behave as if their rate of counting depends on their velocity with respect to the geocentric (non-rotating) frame of the earth, as if this frame is a preferred velocity frame. This could only happen if the speed of light is constant only with respect to the geocentric frame (neglecting the effect of altitude). Conclusions The conclusion that we reach is that velocity time dilation, like gravitational time dilation, is an artefactual change in the rate of caesium clocks, and does not represent any real change in the rate of absolute time. The velocity of caesium clocks with respect to the preferred geocentric frame of the earth determines how much their count rate slows down, most likely because the speed of light with respect to the moving clock has slowed down in order to be constant in the preferred frame. The ability of a sidereal time clock to count exactly the same duration of time for both observers shows that the concept of spacetime, and its antecedent, time dilation, need to be seriously reconsidered. |