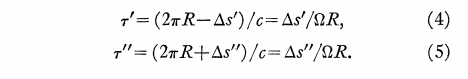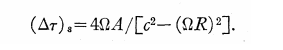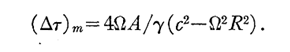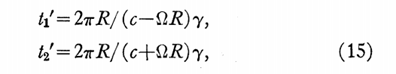The Sagnac Effect: Does it Contradict Relativity? By Doug Marett 2012 A
number of authors have suggested that the Sagnac effect contradicts the
original postulates of Special Relativity, since the postulate of the
constancy of the speed of light is violated in rotating systems.
[1,2,3] Sagnac himself designed the experiment of 1913 to prove the
existence of the aether [4]. Other authors have attempted to explain
the effect within the theoretical framework of relativity, even going
as far as calling the effect “relativistic”.[5] However, we seek in
this paper to show how the Sagnac effect contravenes in principle the
concept of the relativity of time and motion.
To
understand how this happens and its wider implications, it is necessary
to look first at the concept of absolute vs. relative motion, what the
Sagnac effect implies about these motions, and what follows logically
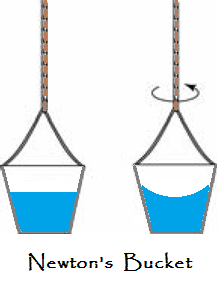
about the broader notions of space and time. Early Ideas Regarding Rotation and Absolute Motion: The fundamental distinction between translational and rotational motion was first pointed out by Sir Isaac Newton, and emphasized later by the work of Ernest Mach and Heinrich Hertz. One of the first experiments on the subject was Newton’s bucket experiment of 1689. It was an experiment to demonstrate that true rotational motion cannot be defined as relative rotation of a body with respect to surrounding bodies – that true motion and rest should be defined relative to absolute space instead. In Newton’s experiment, a bucket is filled with water and hung by a rope. If the rope is twisted around and around until it is tight and then released, the bucket begins to spin rapidly, not only with respect to the observers watching it, but also with respect to the water in the bucket, which at first doesn’t move and remains flat on its surface.
Eventually, as the bucket continues to spin, the water starts to rotate as well, as can be seen from the concave shape of its surface. This concaving of the water shows that it is rotating, even though it is now at rest with respect to the co-rotating bucket. Newton pointed out it is not the relative motion of the bucket and water that causes the concavity of the water. The concaving of the water suggests that it is rotating with respect to something else, far more remote. In Newton’s thinking, this showed rotation relative to say…absolute space. This is contrary to the idea that motions can only be relative. Now
an observer who is sitting in the bucket and thereby rotating with it
can see that the water is concave but may not be able to see or feel
that he is rotating with respect to the surroundings, so the cause of
the concavity may not be obvious, particularly if the rotation is slow
and his view of the surroundings is blocked. On the other hand, an
observer who is standing near the bucket (stationary) will see a
concave shape of the water’s surface that is consistent with his
observation of the bucket rotating in front of him. So although both
observers see the effect of rotation (concave surface) they cannot
necessarily agree on the cause. It
is sometimes argued that because a stationary frame can be identified
(the observer near the bucket), there is no reason to ask “rotating
with respect to what?” However, we wish to show that although multiple
stationary frames can be identified depending on the circumstances,
there is only one truly unique stationary frame, and this is the frame
of absolute space, a.k.a “the fixed stars.” The
Sagnac Effect: While
originally these ideas were applied to mechanical effects, with the
Sagnac effect it becomes clear that the same principles apply to light,
and the frame of reference in which light speed can be shown (or not
shown) to be constant. Consider
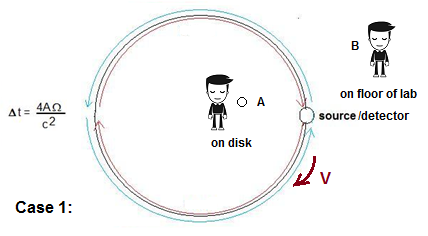
the Sagnac effect in the context of Newton’s bucket experiment. Instead
of a rotating bucket, we have a rotating disk, and on the rim of the
disk are two light paths originating from a source, one going clockwise
and the other going counter-clockwise around the rim of the disk, and
returning to a detector where their time of flight is measured. Since
the transit time is usually very small, the differences in the return
times are determined by a phase difference between the two returning
beams. For the Sagnac effect, we call this Case 1. The speed of light
(C) in the stationary frame is assumed to be C ~= 3 x 108
m/s. If
we now rotate the disk clockwise at velocity v, we find that the blue
beam arrives back at the detector before the red beam – in fact, the
difference in the velocity of
light
turns
out to be 2*v, because the blue beam travels at C+v and the red beam at
C-v. Just
like the concave water, all observers agree that the blue beam has
arrived before the red beam, but again, like in the case of Newton’s
bucket, the explanation of why depends on the perspective of the
observer. For the
observer B it appears
that the detector has approached the oncoming blue beam and has receded
from the red beam, and it is the path length change with respect to the
two beams that accounts for the apparent difference in the speed of
light. On the other hand, the observer at A who is rotating with the
disk has observed that the source and detector are stationary from his
perspective, as are the paths, so he can only conclude (assuming no
foreknowledge that he is rotating) that the light has actually
travelled at two different velocities around the disk, being C+v and
C-v. Who is right?
Well, the problem is
this – from the point of view of special relativity, there are no
preferred frames of reference, there are only relative frames of
reference, so we can’t argue that frame B is better than frame A
without defeating the underlying premise of the theory. In special
relativity (SR), the position of the observer is supposed to be
arbitrary. However, if we accept that perspective A is legitimate, we
defeat the first postulate of SR, namely: “that
light is always propagated in empty space with a definite velocity c
which
is independent of the state of motion of the emitting body”. – Einstein
[7] Further,
on the relativistic notion that ”it is impossible to detect motion by
measuring differences in the speed of light”, as had seemingly been
proven by the Michelson-Morley experiment, the Sagnac experiment shows
that this can in fact be done. Also, observer A can determine that it
is he who is rotating, and not his surroundings. Now to address the idea of stationary states we need to ask the following question: Is there a single unique observer (frame of reference) for which the speed of light is always constant in a Sagnac interferometer? In fact, the speed of light measured by observer B is not exactly constant either, a conundrum which we will explain below.
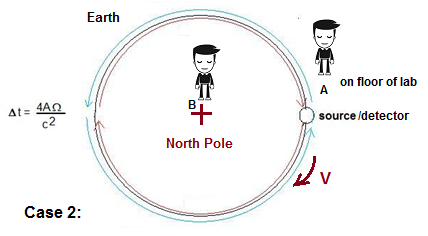
In
case 1 we recall that observer B in the lab was stationary and noted
that the speed of light should be approximately C in both directions.
Let’s expand our interferometer now to encompass the earth. We move our
observer B to the North Pole, where he hovers, not rotating, and our
observer A is placed in the lab on the earth’s surface, along with our
source and detector. Our circular light path is now the equator of the
earth. This configuration is in fact the experiment first proposed by
Albert Michelson in 1904.[6] Since the source, detector, and observer A
are all on the surface of the earth, from their perspective they are
stationary (excluding fore-knowledge). However, as before, A observes
the speed of light reaching the detector after traveling around the
globe to be C+v
and C-v for the blue and red light paths, respectively, where v is the
rotational velocity of the earth on its axis (465 m/s). Also, observer
B at the North Pole can see the Earth rotating under him, so from his
perspective the paths are again unequal and the speed of light is about
constant from his perspective. So
now we can see that the lab frame is not a unique perspective – in case
1 the speed of light was approximately constant in the lab frame, in
case 2 it is variable. However, even in case 1, the so called
“stationary observer” in the lab will be able to detect the slow
rotation of the much smaller lab-sized ring due to the earth spinning
on its axis, of up to 15 degrees per hour, so the speed of light
measured by this observer will not be constant either, but will differ
by the much smaller amount C+/- (r * W)
where r is the radius of the loop and W
is the angular velocity of rotation at the observer’s latitude. However,
the North Pole could be construed as an approximately stationary
perspective for both case 1 and 2. So is the speed of light always
constant with respect to the non-rotating Earth (the so called ECI
frame used in GPS)? Again, we can show this not to be true.
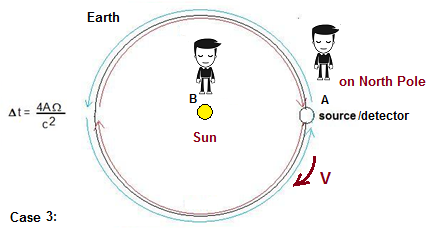
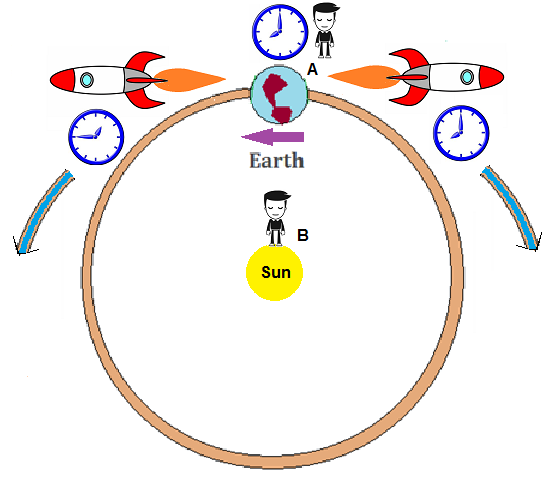
If
we consider a third scenario (Case 3), where B is on the Sun and A is
on the North Pole, and the light paths go around the orbit of the
Earth, we find that now the North Pole perspective sees a variable
speed for C (+/- the orbital velocity of the earth which is ~30 km/s)
and only the observer on the sun sees an approximately constant C based
on his observation that the two light beams have followed longer or
shorter paths. But using the same reasoning as in case 2, the observer
B on the sun will not measure exactly C either, but C+/- a much smaller
value, again being C+/- (r * W)
where r is the radius of the galaxy to our sun and W
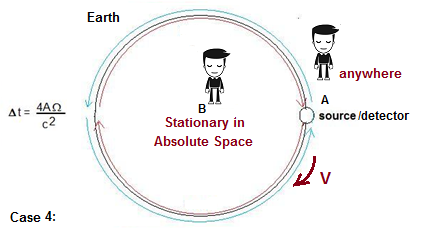
is the angular velocity of our sun around the galaxy. This line of reasoning can continue to be expanded to larger and larger scales – for example, if A is standing on the Sun and B is at the center of the galaxy, then the center of the galaxy becomes the (approximate) preferred perspective. In fact, the only way that we can define an observer for which all circumstances the speed of light C is exactly constant in a circular path, is to place the observer B stationary with respect to the universe.
Any
light following a circular path with respect to B will always be
observed to be exactly C, but only from this perspective. For all other
velocity frames, the speed of light can be variable. In reaching this
conclusion, we have established that the Sagnac interferometer implies
that there must exist only one unique frame of reference for rotation,
and this is the universe itself – absolute space, a.k.a. “the fixed
stars”. So to
answer the question “with
respect to what does the Sagnac interferometer rotate?” we must answer,
“absolute space, the fixed stars.” But in doing so, we are compelled to
reject the idea of the relativity of motion that is the cornerstone of
Einstein’s theory.
______________________________________________________________________________________________
The
Non-Relativity of Time
The
Sagnac effect also does for time what it does for light. Many of us
know Einstein’s famous twins paradox, where one twin stays on earth
while the other travels in a rocket at near light speed, returning
years later to meet his twin. When they meet again, the travelled twin
is younger than the stay at home twin, because according to Einstein,
the high velocity of the second twin meant that time progressed slower
for him than the stay at home twin. This
thought experiment was criticized by Dingle,[8] who aptly pointed out
that if Einstein argues that a moving clock counts slower than a
stationary one, but also presumes all motion to be relative, then we
should be able to argue with equal justification that it is the
earthbound twin who has moved away at velocity from the rocket bound
twin, and that the former’s clock has counted slower instead. An attempt to
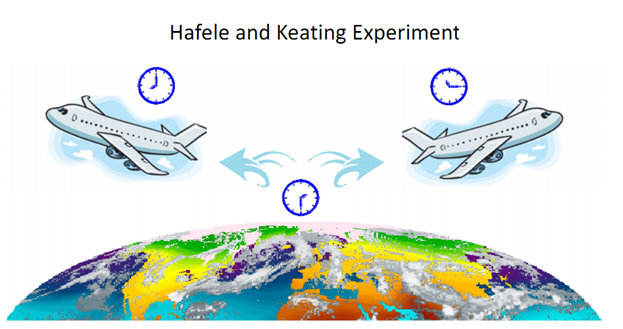
resolve this issue was the Hafele and Keating Experiment.
Hafele and Keating
[9,10] performed an experiment in 1971 to test Einstein's predictions
regarding the dilation of time in clocks moved at some velocity with
respect to a stationary clock. In the opening statement of the first of
two papers on the subject, the authors refer to the debate surrounding
the "twins
paradox" and how an experiment with macroscopic clocks might provide an
empirical resolution. In Hafele and Keating's experiment, they flew
cesium clocks around the world in opposite directions near the equator,
and then measured how much time they have gained or lost when they
return to the start point as compared to a stationary cesium clock to
which they were originally synchronized. The experiment of Hafele and Keating
(HK) actually differs from the twins paradox in some important ways -
firstly, in the paradox, the traveling twin moves in a straight line to
a distant point then turns around and comes back, with a series of
accelerations and decelerations. In the HK experiment, the journey is
circular and the clocks never leave the earth’s influence. In following
a circular path, the HK experiment becomes a Sagnac effect experiment
where it is clocks that are moving rather than beams of light.
From
the perspective of the observer on the ground, the moving clocks of Hafele and Keating
have experienced similar motions with respect to the stationary earth
bound clock. If their motions were truly "relative", then by the rules
of SR both should arrive back at the starting point having experienced
the same amount of time dilation in the same direction. The
actual result was that one travelled clock increased in its time rate
and the other decreased. This is the identical result to what would be
expected for light in the Sagnac experiment Case 2, where one beam
travels faster than expected, and the other slower than expected. And
as before, it implies that the only observer who sees all clocks count
at a rate proportional to their velocity is the observer at the North
Pole, who is in the non-rotating, geocentric (ECI) frame of the earth.
As Murray pointed out, Hafele and Keating
interpreted their result by following a revised form of relativity
attributable to Builder, who they reference in their first paper in
1971. In Builder's "Ether and Relativity" he summarizes his view
as follows [12]:
"The
relative retardation of clocks, predicted by the restricted theory of
relativity, demands our recognition of the causal significance of
absolute velocities. This demand is also implied by the relativistic
equations of electrodynamics and even by the formulation of the
restricted theory itself. The observable effects of absolute
accelerations and of absolute velocities must be ascribed to
interaction of bodies and physical systems with some absolute inertial
system. We have no alternative but to identify this absolute system
with the universe. Thus in the context of physics, absolute motion must
be understood to mean motion relative to the universe, and any wider or
more abstract interpretation of the "absolute" must be denied.
Interactions of bodies and physical systems with the universe cannot be
described in terms of Mach's hypothesis, since this is untenable. There
is therefore no alternative to the ether hypothesis. "
Builder’s
conclusion that there must be "an absolute inertial system"
re-introduces the preferred frame of Lorentz back into relativity, the
very thing that Einstein sought to eliminate.
If we are to accept Builder's
hypothesis of a universal preferred frame for motion (ether), then we
are compelled to accept the other critical tenet of Lorentz over
Einstein, that it is the speed of light, and not time, which is the
fundamental variable in our universe. In accepting a notion of absolute
motion, or a preferred frame, we are as Dingle says, rejecting the
notion of "relative motion". Despite Einstein borrowing heavily from
Lorentz's equations and theory, and the fact that both theories predict
similar results for the same experiments, the two theories are
philosophically antithetical - and as such the conclusions about the
nature of space and time result in entirely different models of the
universe. Let’s look at the implications of the Hafele and Keating Experiment on the relativity of time. Similar to our original case 3, we expand the travelling clock experiment to the orbit of the earth. Rather than planes, we put cesium clocks on two rockets and have them take off from the surface of the earth at equal escape velocities (say 12 km/s), but set to travel in opposite directions around the sun before returning to the earth, as in the figure below. The rockets maintain the same velocity with respect to the earth’s surface throughout their voyage. Both rockets arrive back on the earth at around the same time, and again at the same velocity with respect to the earth, at 12 km/s. As expected, the rocket on the left going counter-clockwise arrives with its clock rate slowed with respect to the earth clock, and the rocket on the right travelling clockwise has had its clock rate sped up with respect to the earth clock, even though their velocity with respect to the earth’s surface clock was the same. From the perspective of the earth (assuming no foreknowledge that they are rotating), the path lengths for each rocket
Again, we can
extrapolate this thought experiment to the edge of the galaxy, and
further to the entire universe. For
clocks rotating around an observer, the only unique
perspective where ultimately any rotational motion will always
lead to a slowing of the clock rate is the stationary frame of the
universe. In any other velocity frame, it will always be possible to
create orbiting clocks that appear to speed up in rate with respect to
our observer. This is the same conclusion as earlier for the speed of
light, except now applied to time. These
rotation experiments have implied that there is a an absolute space
with which we can define a reference speed of light C, and a preferred
frame of reference for a time clock for which all other moving clocks
will count at a slower rate. Since
Einstein invented the idea of a variable time in order to explain the
constancy of the speed of light, should it not follow then that if we
have shown that the speed of light is not always constant for moving
observers, then perhaps instead it is “time” that is constant, and the
velocity of light is variable depending on
our motion
with respect to absolute space? Since translational experiments always
show a constant measured speed of light, unlike the Sagnac experiment,
perhaps apparent time dilation is our only indirect evidence that the
speed of light is changed in a hidden way during translational motion.
In order to prove this we would need to design a clock that doesn’t
depend on the speed of light in its counting principle, and see if this
clock is unaffected by time dilation. Again, we will turn to the Sagnac
effect and rotation to design such a clock. But first, let’s examine
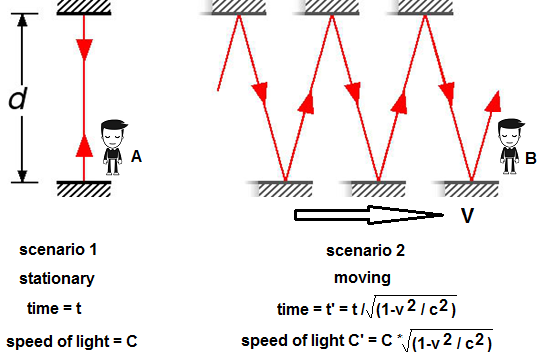
the basis for time dilation in Einstein’s theory. The Light Clock Analogy When we see a supernova explode in the sky, we do not say “that event just happened”, since we know the light from that event has taken perhaps thousands of years to reach us from some distant point in space. We would say, rather, that the explosion happened thousands of years ago. This is because our judgement of the simultaneity of events is independent of the speed of light. Rather the speed of light might be used to insinuate when an event could have happened in the past, based on the propagation delay. So why then would we believe that the rate of time itself depends on the speed of light? Consider Einstein’s analogy, often reproduced, of a light beam bouncing between two mirrors. In his analogy, two horizontal mirrors face each other and one mirror is spaced above the other by a distance d. A light pulse bounces vertically between the two mirrors as shown on the left. The time it takes for the pulse of light to do a round trip (from the top mirror to the bottom and back) is twice the distance d divided by the speed of light. This is his light clock.
Suppose
the "light clock" were traveling sideways at a very high (but constant)
speed of 0.5 C. Now the pulse would follow the "saw tooth" path shown
on the right side of the drawing. Since light speed is the same as
before (remember, the speed of light is not changed by the speed of its
source), it will take longer to make a round trip. So our "light clock"
takes longer to count out its intervals. Another way of saying this is
that the clock "ticks" more slowly. But
here lies the problem. This analogy works because the speed of light is
constant as seen by observer A. From his vantage point, he can see both
clocks working, and although the speed of light is travelling at the
same rate in scenario 2, it has taken a longer path to hit the moving
mirrors. In taking a longer path, it has taken more time to reach the
end (based on A’s clock – 1.1546 x longer or t/0.866 = t’). But because
we have already said that the rate of time is independent of the speed
of light, we cannot assume that “real” time has passed slower for
observer B than observer A, we can only conclude that B’s clock has
counted mechanically slower because it has taken longer for the light
to travel the distance between scenario 2’s mirrors. Now, if observer B
measures the speed of light in his moving frame using “real” time, i.e.
a clock not affected by the speed of light,
he should
conclude that the speed of light is slower than C, namely 0.866*C = C’.
This is exactly like the situation of the Sagnac interferometer –
observer B is unaware that he is moving, so he perceives the mirrors to
be opposite each other and separated by distance d, so he would measure
the speed of light to be less than C. He is unaware that from the
perspective of observer A, the path d has lengthened. So why does he
conclude that the speed of light is instead C? This is because he
measures the time elapsed using a clock that is based on the length of
time it takes for light to pass between his own moving mirrors. In
effect, his moving clock is calibrated by the speed of light seen in
his own frame (which is 0.866*C), so consequently, his clock counts
slower by exactly this amount (t/0.866). This makes him falsely measure
that the light beam to have arrived at velocity C rather than C *
0.866. If the
speed of light was actually
C in his frame, i.e. C = C’, then his moving light clock would count
faster (now t = t’) then although he would still measure the speed of
light to be C with his clock, the time rate difference between A and B
would disappear! Since the slowing of clocks (apparent time dilation)
does occur in reality, this implies, just like in the Sagnac
experiment, that the speed of light is only actually C in the
stationary frame, and in the moving frame it is actually C * We
can go one step further – the light clock analogy explains why every
translational experiment to measure the speed of light shows that the
speed of light is always C – because the clocks used to measure C are
calibrated to the speed of light in their frame, this built-in
correction factor always adjusts the measured speed back to C. However,
in every rotational experiment, it is trivial to measure a speed of
light that is not C. This is because, as we showed with Hafale and
Keating, clocks moving in rotating paths around a disk or sphere will
go out of synchronization with each other – using a common origin as a
reference and a circular path to the detector confounds the
self-correcting ability of a light clock, and the underlying difference
in the speed of light with respect to the origin is revealed. The
Sagnac Clock: As we said
earlier, in order to prove that time dilation is an illusion, we
would need to design a clock that does not depend on the speed of light
in its counting principle, and see if this clock is unaffected by time
dilation. Again, we turn to essential feature of the Sagnac effect,
rotation, to design such a clock. This concept was first proposed in
our article “The
Paradox of the Clocks in the Canaries”
in 2010. The
simplest time dilation effect to test is gravitational time dilation,
the speeding up of clocks with altitude. According to Einstein, the
rate of time follows the gravitational potential, so a clock on the
surface of the earth should count more slowly than a clock at some high
altitude, such as at the top of a mountain. Time is alleged to be
moving into the future faster at the top of a mountain.
So we
need a clock on the Earth that is unaffected by altitude. Let's say we
use the rotation of the earth as our clock instead of a conventional
cesium clock. After all, our human concept of time, and the units that
compose it (days, hours, minutes, seconds) are already derived from the
rotation period of the earth, so it should be the ideal clock for
comparison. For each observer, we could use as our reference the
position of the sun in the sky, or the position of a Foucault pendulum,
or most preferably the position of the fixed stars in sidereal time. If
we measure the sidereal day (23.93447 hours) as the time for one earth
rotation relative to the vernal equinox, using a sighting star as a
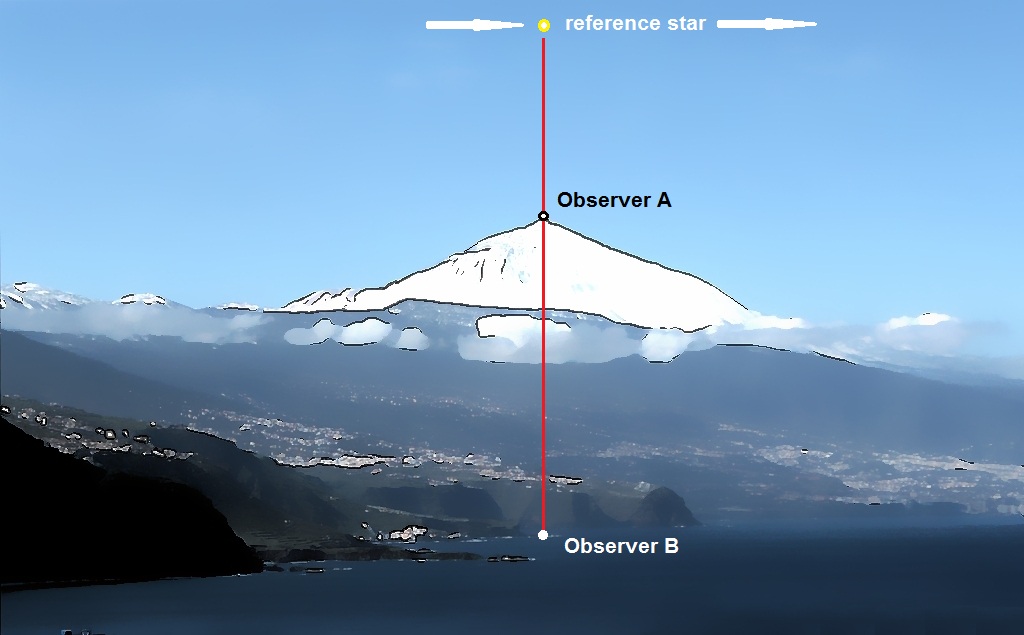
reference, we can then place an observer A at the top of a mountain,
and another observer B at sea level. Preferably the mountain observer
is exactly vertical over the sea level observer, and this vertical line
passes through the center of the earth, as shown in the picture below.
We use as our example the mountain Pico del Teide on Tenerife, with an
altitude of 3718 meters. We give each observer A and B a cesium clock,
and a sidereal clock. The
sidereal clocks
mark a tick when the reference star is directly overhead each day. The
cesium clocks mark a tick when 23.93477 hours has passed in their local
time. We then compare the four clocks to determine if they are counting
at the same rate. What happens is that when the reference star passes over the red vertical line passing through observer A and B, both sidereal clocks have no choice but to trigger at the same moment, differing only in the light propagation time between A and B. Because this propagation time is a fixed amount, it does not affect the rate at which the two clocks count – therefore the count rate is exactly the same. However, since both cesium clocks experience gravitational time dilation, the cesium clock at observer A must count faster than the cesium clock at observer B. If we had pre-synchronized the two clocks at sea level, then the cesium clock at observer A will begin to go out of synchronization with
the
other three clocks, and the amount of time gained by cesium clock A
will continue to increase as the days pass. Clearly three of the 4
clocks agree on the amount of elapsed time – only cesium clock A reads
in error. The fact that we have created clocks immune to time dilation
implies that real time has never changed at the top of the mountain – apparent
time dilation is an artifact of the difference in the speed of light at
two difference points in space, and the use of clocks calibrated to the
speed of light – i.e. the light clocks of Einstein. This
conclusion is also consistent with our reason – given the millions of
years that the mountain has been around, the summit of Pico del Teide
should by now be several minutes in the future compared to the land at
its sea shore base. And yet they are physically
connected.
To believe that time dilation is real would require us to assume that
walking up the mountain is the same as walking into the future - the
land would have to form a bridge between two points in Einstein’s
dimension of time. It
is somewhat trivial
to travel to the top of the mountain and view through a telescope a
clock tower in Puerto de la Cruz far below to verify that the top of
the mountain and the sea side resort share the same present.
The
author at the summit of Pico del Teide in 2012, checking the time.
Puerto de la Cruz is clearly visible 3718 meters below. Still in the present…
Conclusions: It is often argued that the predictions of Special and General Relativity have been continuously verified and that therefore the theory is unquestionable. However, other theories, such as Lorentz ether theories modified to take into account gravitational effects, can also make similar claims. There are in fact multiple mathematical routes by which a correct prediction can be arrived at, but these theories may imply very different interpretations of what our physical reality is. And this is at the heart of what is wrong with the theory of relativity – it may make successful predictions based on math, but implies a nature of time and space which are not only inconsistent with logic and reason, but are even contradictory. Our interpretation is that these problems arise because of the switch from the absolute time / variable speed of light of Lorentz (1904) [13] to relative time / absolute speed of light of Einstein (1905) – two stances which are only slightly different mathematically. In Lorentz’s favour, the Sagnac effect demonstrates that depending on the placement of the observer, it is possible to see this variable speed of light and to confound apparent time dilation. Our analysis of Einstein’s light clock has shown that it will always count in error if the speed of light is not C in the moving frame. And further, our thought experiment with sidereal clocks has shown that the entire premise that time dilation corresponds to a change in “real” time is highly questionable. So when countered with the argument that General Relativity can explain the Sagnac effect, we might ask, why bother? If time dilation is an illusion, then the entire 4D time-space continuum of Einstein should be considered, to use his own word for the aether, “superfluous.”[7] References: [1] Moon, Parry,
Spencer, Domina Eberle, and Uma, Shama, (1991)
The
Sagnac Effect and the Postulates on the Velocity of Light. [2] Ruyong Wang (2003)
Modifed
Sagnac experiment for measuring travel-time difference between
counter-propagating light beams in a uniformly moving fiber. [3] Alexandre Dufour, Fernand
Prunier
(1942)
On the Fringe Movement Registered on a Platform in Uniform Motion [4] Georges Sagnac (1913)
Regarding the Proof for the Existence of a Luminiferous Ether using a
Rotating Interferometer Experiment. [5] Rizzi, Guido, (2003)
The Relativistic
Sagnac Effect: two derivations.
[6] A. Michelson, (1904) "Relative
Motion of Earth and Aether." Philosophical
Magazine (6), 8, 716-719. [7] Albert Einstein
(1905)
On the Electrodynamics of Moving Bodies. [8] Herbert Dingle (1980) The Twins Paradox of Relativity.
[9] Hafele, Joseph C.; Keating, Richard E. (July 14, 1972). "Around-the-World Atomic Clocks: Predicted Relativistic Time Gains". Science 177 (4044): 166–168. Bibcode 1972Sci...177..166H. doi:10.1126/science.177.4044.166. PMID 17779917.
[10] Hafele, Joseph C.; Keating, Richard E. (July 14, 1972). "Around-the-World Atomic Clocks: Observed Relativistic Time Gains". Science 177 (4044): 168–170. Bibcode 1972Sci...177..168H. doi:10.1126/science.177.4044.168. PMID 17779918.
[11] Murray, W.A.
Scott, "If you want to know the time..."
Wireless World.
92 No.16 28-31 1986. [12] Geoffrey Builder
(1957) Ether
and Relativity. [13] Hendrick Lorentz (1904)
Electromagnetic phenomena in a system moving with any velocity smaller
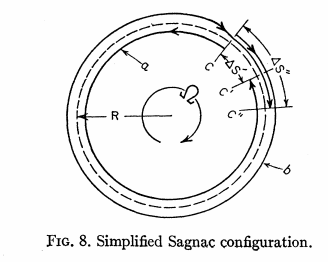
than that of light. Appendix A Post’s Kinematic explanation of the Sagnac Effect: E.J. Post [19] uses the stationary observer position where the speed of light is assumed to be c, and then works backwards to try to show that the moving observer’s measured result is the same. From the point of view of the stationary observer: Position
C = origin/detector Ds’
= distance C has rotated clockwise by the time the counter-clockwise
beam reaches it at C’ Ds”
= distance C has rotated by the time the clockwise beam reaches it at C” c = free space speed of light.
Time difference for each path t’ = counter-clockwise, t” = clockwise
From the stationary observer’s point of view, the time difference is then:
The
time interval of the rotating beam splitter is then computed to be:
Where g
corresponds to the time dilation factor due to the rotational motion. However,
does the relativistic correction to the Sagnac equation actually make a
difference in the actual result? When we consider the rotating Sagnac
interferometer as a device experiencing time dilation, we need to
consider first which parts are clocks and what the actual outcome time
dilation will have on the measuring system, the detector. Let’s look at
the Sagnac interferometer as three parts: a)
A
source such as a laser, which is a light clock subject to velocity time
dilation b)
An
optical path composed of wavelengths of the emitted light c)
A
detector, which measures the phase difference between the wave-fronts
of the two returning beams. The source (for example a laser) is a true clock – lets assume that this clock experiences a time dilation proportional to
t’
= to/SQRT(1-WR^2/c^2)
= to
* b
. then, Dt
= to * b
- to = (2L- 2L/b)/C
(1) This will inevitably mean
that the rotating source must emit light at a reduced frequency,
proportional to f’ = f * SQRT(1-WR^2/c^2).
However, since C = f*l,
the wavelengths in the optical path must expand due to the lower
frequency. This means that there will be fewer wavelengths passing the
detector per unit time. The
difference will be in the amount of time a given wave-front is now
behind compared to the unaffected laser situation: Dt
= (2L- 2L/b)/C
(2) So the wave-fronts are
behind by the amount Dt.
But as we showed in 1, the time is also behind by the same amount Dt
since the duration of each second is larger due to the clock frequency
change. The result is that the two effects cancel out, and the same
wave-front arrives at the detector at the same elapsed time regardless
of the time dilation, from the standpoint of the observer on the disk.
The relativistic correction would seem thereby to be unnecessary. As
Post says, the result is too small to be experimentally
distinguishable, and the common practice is to use a g
factor = 1. So
this in and of itself does not contradict the notion that the measured
speed of light by an observer on the disk is C +/- WR.
Post
says himself that “the circulation times t1’ and t2’ in the rotating
frame are obtained by integrating f’
from 0-2p
and
0- -2p,
respectively:
And
then it is easy to see that in the rotating frame: Dt
= L/(C+WR)
– L/(C-
WR)
= 4AW/c^2
(3) Post
quotes the method of Langevin from his 1921 and 1937 papers. In his
1921 paper, Langevin argued that because the Sagnac effect was first
order, there could be no distinction between Newtonian or relativistic
derivations and therefore the effect was in accordance with relativity
theory. Dufour and Prunier took Langevin to task on this. Dufour and
Prunier’s work is discussed by Kelly [17] in his book “Challenging Modern Physics: Questioning
Einstein's Relativity Theories”. In
their experiments they created Sagnac interferometers that were
composites of moving and stationary paths, including stationary sources
and stationary detectors. This was essentially to test if the
relativistic approach could be distinguished from the classical
approach. In particular, they focused on the mathematical treatment of
Langevin, whereby the position placement of the observer on the disk is
arbitrary. Using Langevin’s calculation: Dt
= L/C + 2WA/C^2
(4) They
predicted that in a Sagnac interferometer where only part of the light
path was rotating and the other part stationary, the classical equation
would call for a different area A than the relativistic equation for
calculating the result. In
all cases of this experimental test, the Sagnac effect was the same.
This overturned Langevin’s
analysis, and in 1937, [14] he had to revise his explanation, as
pointed out by Kelly: “In
his final essay on the subject in 1937, Langevin proposed that the
results published that year by Dufour and Prunier showed that one had
to assume either (a) the light speed varied to c + wr
in one direction and c – wr
in the other direction, or (b) the time aboard the spinning apparatus
had to change by a factor of +/-2wA/c2
in either direction. Indeed, Langevin went as far as to say that
assuming (a), “we
find, by a very simple and very general reasoning, the formula for the
difference of the times of the path of the two light beams in the
Sagnac experiment.” He also stated that “the paths are of unequal
length because of the inequality of the speed of prorogation”.
The
proposition (b) though is untenable because if this were true then when
the light beam passed back to the moving detector, the local time from
each direction would be out of synchronization, meaning that the clocks
cannot be counting real time and that the effective time dilation is
meaningless. This was also pointed out by Herbert Ives in his 1938
paper
[16] criticizing Langevin. Ives says about the absurdity of Langevin’s
proposition (b): ”
There are of course not merely two clocks, but an infinity of clocks,
where we include those that could be transported at finite speeds, and
around other paths. As emphasized previously, the idea of “local time”
is untenable, what we have are clock readings.
Any number of clock readings at the same place are physically possible,
depending on the behaviour and history of the
clocks used. More than one “time” at one place is a
physical absurdity. “ The
only explanation left, is Langevin’s proposition a) that the light
speed varies by C+/-wr
in one or the other direction around the disk, consistent with Dufour
and Prunier’s experimental results. References:
[14]
Paul Langevin – (1937) On
the Experiment of Sagnac.
Compt. Rend. 205, 51. [15}
Paul Langevin – (1921) Compt. Rend. 173, 831. [16]
Herbert Ives - (1938)
Light Signals Sent Around a Closed Path. [17]
Al Kelly, Challenging Modern Physics: Questioning
Einstein's Relativity Theories”. [18]
A. Dufour, F. Prunier, On
a Fringe Movement Registered on a Platform in Uniform Motion (1942). [19]
E. J. Post, Sagnac
Effect,
Review of Modern Physics, 39,2, |