Did the Hafele and Keating Experiment Prove Einstein Wrong? V.
Bobblehead Productions, 2013 Hafele and
Keating performed
an experiment in 1971 to test
Einstein's predictions regarding the dilation of time in clocks moved
at some
velocity with respect to a stationary clock. In the opening statement
of the
first of two papers on the subject, the authors refer to the debate
surrounding
the
"twins paradox"
and how an experiment with macroscopic clocks might provide an
empirical
resolution. In Hafele and Keating's experiment, they flew cesium clocks
around
the world in opposite directions near the equator, and then measured
how much
time they have gained or lost when they return to the start point as
compared
to a stationary cesium clock to which they were originally
synchronized. The
experiment of Hafele and
Keating (HK) actually differs from
the twins paradox in some important ways - firstly, in the paradox, the
traveling twin moves in a straight line to a distant point then turns
around
and comes back, with a series of accelerations and decelerations. In
the HK
experiment, the journey is circular and the clocks never leave the
earth’s
influence. In following a circular path, the HK experiment becomes a
Sagnac
effect experiment where it is clocks that are moving rather than beams
of
light.
From the perspective of the
observer on the ground, the moving clocks of Hafele and
Keating have experienced similar
motions with respect to the stationary earth bound clock. If their
motions were
truly "relative", then by the rules of SR both should arrive back at
the starting point having experienced the same amount of time dilation
in the
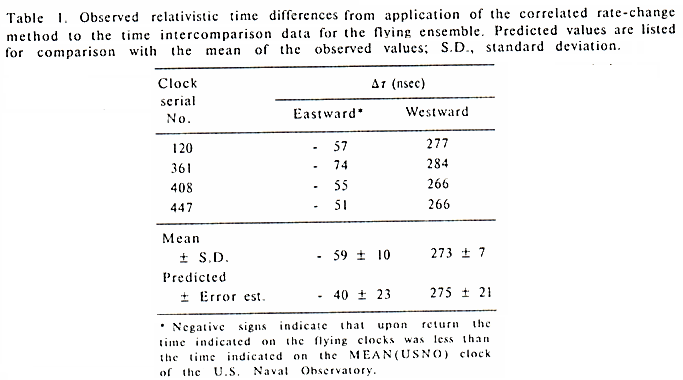
same direction. The actual result was that the westward travelled clock
increased in its time rate (more time had elapsed) and the eastward
travelled
clock decreased in its time rate. The
result was as follows from their 1972 paper in Table 1:
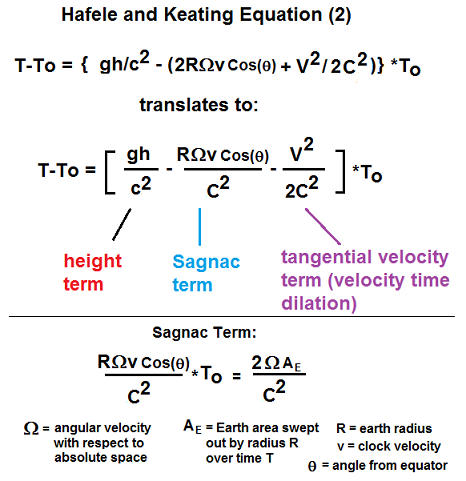
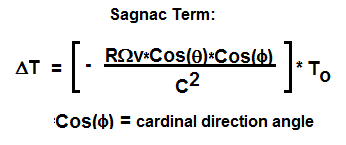
The expected time dilation
on clocks used by Hafele and Keating is shown below in Fig. 2. This
consisted
of a height term gh/c^2, a velocity time dilation term v^2/2c^2, and a
third
term RΩvCos(θ)/c^2 which will herein be
referred to as the “Sagnac term”. The height and velocity terms were
predicted
by Einstein in 1907 and 1905 – however the Sagnac term was unknown to
Einstein
when he wrote his papers on special relativity, so this effect was
never
anticipated by Einstein. This effect became incorporated awkwardly into
Hafele
and Keating’s relativistic calculations with the following comment: “Because the earth rotates,
standard clocks distributed at rest on the surface are not suitable in
this case
as candidates for coordinate clocks of an inertial space. Nevertheless,
the
relative timekeeping behavior of terrestrial clocks can be evaluated by
reference to hypothetical coordinate clocks of an underlying
non-rotating
(inertial) space (6). “ In note (6) they further explain: “It is
important to
emphasize that special relativity purports to describe certain physical
phenomenon only relative to (or from the point of view of) inertial
reference
systems, and the speed of a clock relative to one of these systems
determines
its timekeeping behavior. [G. Builder, Aust. J. Physics 11, 279
(1958)].
Although inertial systems are highly specialized, they have an
objective
physical relationship with the universe because they have no
acceleration or
rotation relative
to the universe. “ (my itallics
added). The clarification comes
from Builder's "Ether
and Relativity" as
follows: "The relative
retardation of clocks, predicted by the restricted theory of
relativity,
demands our recognition of the causal significance of absolute
velocities. This
demand is also implied by the relativistic equations of electrodynamics
and
even by the formulation of the restricted theory itself. The observable
effects
of absolute accelerations and of absolute velocities must be ascribed
to
interaction of bodies and physical systems with some absolute inertial
system.
We have no alternative but to identify this absolute system with the
universe.
Thus in the context of physics, absolute motion must be understood to
mean
motion relative to the universe, and any wider or more abstract
interpretation
of the "absolute" must be denied. Interactions of bodies and physical
systems with the universe cannot be described in terms of Mach's
hypothesis,
since this is untenable. There is therefore no alternative to the ether
hypothesis. " We say “awkwardly” because
in order to incorporate this Sagnac term, Hafele, Keating and Builder
make some
categorically un-relativistic statements, namely:
1) Inertial motion can only be
referenced to the physically privileged frame of the “universe” which
is an
absolute inertial system.
2) The “absolute velocities”
must mean motion with respect to this absolute frame of reference.
3) There is no alternative to
the ether hypothesis. We will return to these
issues later, but let’s continue to address the Hafele and Keating
equation and
apply it to low speed motions on our terrestrial sphere. The
equation is displayed below: Fig. 2:
Since
we are calculating
time dilation on a rotating sphere we also have to add a term to
correct for
direction, since if a plane or train goes west its velocity subtracts
from
earth’s rotational velocity, if it goes east it adds.
This version is shown below:
Applying
the Hafele and Keating equation to Einstein’s trains: Now,
if we apply this equation to the predictions Einstein’s made in his
special
relativity theory (SR) about time dilation in clocks on moving trains,
we
discover that his original predictions would appear to be in error. We will restrict ourselves
in this discussion
to the case where the trains travel at the same sea level altitude, so
gravitational time dilation need not be considered. Fig. 2:
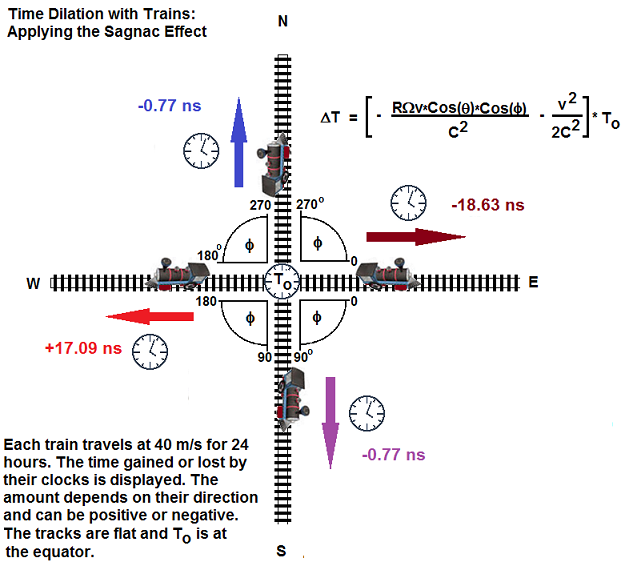
As
can be seen from the above figure, the total amount of time dilation
experienced by each train travelling at the same speed depends on
the cardinal direction. The clock on the train
travelling
east counted slower compared to the stationary clock at To. The clock
on the train travelling west counter faster. The time lost on
the
eastbound train was 20X higher than that lost on the north and
southbound trains.
Einstein
Prediction 2:
"If one of two synchronous clocks at A is
moved in a closed curve with constant velocity until it returns to A,
the
journey lasting t seconds, then by the clock which has remained at rest
the
traveled clock on its arrival at A will be 1/2 t v^2/c^2
second slow. Thence we conclude that a balance-clock at the equator
must go
more slowly, by a very small amount, than a precisely similar clock
situated at
one of the poles under otherwise identical conditions. See " On the
Electrodynamics of Moving Bodies 1905
p. 11. This prediction is actually
disproved by the Hafele and Keating experiment proper, since the
travelled
clock obeys equation (2) above. As a consequence, the
travelled clock
experiences either a gain or a loss of time depending on whether it
travels
west or east, and this amount is more than the 1/2 t v2/c2
value predicted by Einstein. Einstein
Prediction 3: “If
the principle of relativity were not
valid we should
therefore expect that the direction of motion of the earth at any
moment would
enter into the laws of nature, and also that physical systems in their
behavior
would be dependent on the orientation in space with respect to the
earth.” Ref: A. Einstein, Relativity,
the Special and General
Theory, 1920, P. 17-18. As
shown in Fig. 2, we can see that “the direction of motion of the
earth” actually does figure in the calculation, in the form of the
angular
velocity of the earth W.
Further, the “orientation in space with
respect to the earth” also figures in the calculation, via Cos(f),
since the amount of time dilation depends on whether the trains is
travelling
North, South, East or West along the earth. Einstein Assertion 4: “The introduction of a “luminiferous ether" will prove to be superfluous inasmuch as the view here to be developed will not require an “absolutely stationary space" provided with special properties, nor assign a velocity-vector to a point of the empty space in which electromagnetic processes take place.” See " On the Electrodynamics of Moving Bodies 1905 P.1.
A
consequence of this is that the measured speed of light for the return
journey of the beam from the source to the detector will never be C,
but will actually
be a variable speed of light, which depends on the direction the beam
travels,
the radius R of the light path loop and W*cos(f)
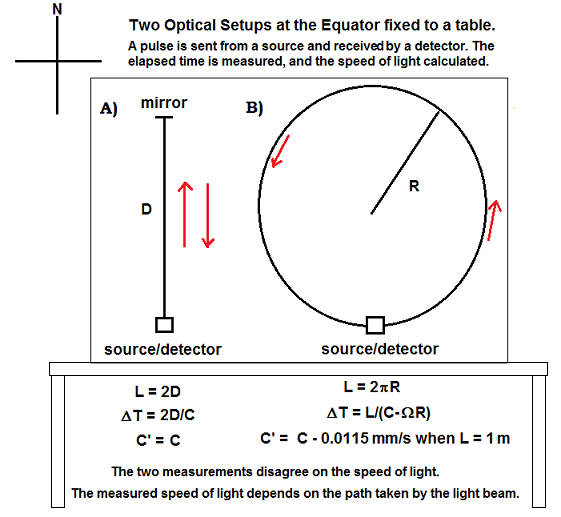
of the earth similar to the situation of fig. 2. Fig.
3:
For
example, if we use the
values above of a vertical loop of length = 1 meter and the table and
observer are at the
equator with a counter-clockwise beam, the speed of light is measured
as C –
0.0115 mm/s. If the beam goes clockwise, the light beam will be
measured to have
exceeded the speed of light! We conclude from this experiment that the
measured
speed of light is not constant. Further, if we consider the two paths A
and B
to be members of a set of closed paths enclosing an area = x, then path
A
represents the condition where x = 0, but path B represents every other
possible value of x up to infinity. So path A, where the relativistic
prediction is met, is the exception, whereas generally, all other
possible
members of the set will be measured to have a variable
speed of light C’ in the laboratory frame – which frankly
is the frame that most often matters. This is similar to the situation
of Fig.
2, where Einstein’s prediction is only approximately true when the
train
travels exactly North or South. The
argument usually goes
that the setup on the right encloses an area and therefore experiences
the
Sagnac effect due to the rotation of the earth, and thereby the table
is not an
inertial frame. However, the two setups share the same frame of
reference - so
either both setups are invalid for SR, or both are valid. If an
argument is
going to be made that a speed of light test is invalid because the
frame is
rotating, or the observer is rotating, then we have to discard all
speed of
light tests to date since every place that humans have performed a test
on the
earth or in near space have always been experiencing some form of
rotation,
either diurnal or orbital, which in modern times has become readily
visible. As Hafele
and Keating say in their paper,
inertial motion must be referenced to a universal reference frame.
Another common argument is to say that the path length has changed due to the rotation and this is why the speed of light is not measured to be C. But for our figure 3B the path length does not change for our laboratory observer since the loop is stationary in his frame. In fact, all observers anywhere on the earth would observe some degree of variable speed of light in the loop except an observer at the earth's pole** – but if we choose this singular position as the only valid observer, i.e. the only one who measures a path change sufficient that C = C’, are we not establishing the pole as a preferred frame of reference over all others? A singular frame where the speed of light is constant, just like in aether theories? Relative inertial frames of reference existed only to the extent that we could not detect their rotation – now that we can routinely detect diurnal rotation in our optical instruments and clocks, can we really say that a purely inertial frame of reference still exists independent of the non-rotating universe?
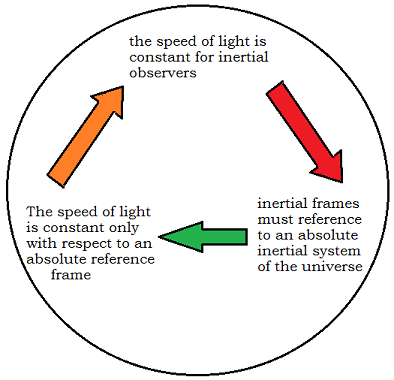
Fig 4: A Sphere of contradiction. If
the speed of light is constant for inertial observers, and inertial
motion is referenced to an absolute inertial system, then the
speed of light is only constant in an absolute reference
system
or in some restricted motion with respect to it. The Hafele and Keating
experiment would appear to oblige relativity to adopt the same
definition as many
ether theories - i.e. the speed of light is constant in a preferred
reference frame similar to the ideas of Lorentz.
Conclusions Although
the
Hafele and Keating experiment did confirm the
gravitational time
dilation
effect on clocks predicted by Einstein, the velocity time dilation
predictions
of special relativity (1905) at low velocities would seem to have been
proven wrong, since the Sagnac term was not accounted for. I
personally do not consider the Sagnac effect relativistic simply
because it involves time dilation - the concept of time dilation was
not conceived of by Einstein, but rather by Lorentz and Larmor.
Further, time dilation can be construed as simply an error in clock
readings, as discussed here.
The Sagnac term is at odds with a fundamental tenet of relativity
theory by requiring an absolute frame of reference
for both
rotational and inertial motion, defining the latter as
relative to
a non-rotating universal frame. Why then has the Sagnac effect been
rebranded as “relativistic”?
Some have cited Max
van Laue
as discussing the effect (after the proposal of Michelson in 1904,
before Einstein
was even known) in terms of special relativity in 1911. What he actually says of it
is that “it's
not possible to decide between the theory of relativity and the
stationary
aether theory by the proposed experiment.” This sentiment was continued
by Silberstein,
who was involved in getting Michelson to perform the Michelson-Gale
Experiment
(via A.C. Lunn). This
is what Silberstein said about relativity and the Sagnac Effect: ”The
special relativity theory is wholly incompetent to deal with the
problem of
light propagation in a rotating system rigorously, simply because it
has
nothing to do with any reference systems other than the Galilean or
inertial
ones, i.e. the fixed star system S*.” Silberstein further said of the
general relativity treatment of the Sagnac effect: “…the relativity
theory is unable to
construct the required line element on its own great principles, and is
content
to transcribe it from the Galilean line element…” So
relativity theory would appear to contribute little to
understanding the effect. However
in the mid-80’s the Hafele and Keating
experiment began to be referred to as a “relativistic Sagnac
experiment”, attributed to Allan,
Weiss and Ashby.
They said that the principle of the constancy of
the speed of light leads to a prediction of the Sagnac effect in
rotating
systems; this is an interesting comment since the constant speed of
light in their example is in the non-rotating frame of
reference -
i.e. the frame of the fixed stars just as in Fig. 4 above.
This
underlines the extent to which "relativistic" has become
interchangeable with "absolute."
Notes: *
Note – the first
reference we can find mentioning that the Sagnac effect is rotation
with
respect to the “fixed stars” for both aether and relativity theories,
is L.
Silberstein’s paper from 1921. **
Even
this doesn’t solve the problem, since a pole observer will still be
rotating
with respect to the fixed stars.
|