Explanation for
the
lack of terrestrial aberration in a Michelson Interferometer: Doug Marett
(2013) Introduction:
Although it is now
widely accepted that a moving Michelson interferometer will experience
no fringe
shifts due to its velocity, a simple analysis of the moving mirrors
with
respect to the laser light does suggest that the beams should undergo
some
slight terrestrial aberration. For example, Janssen
[3] pointed out that the assumptions of Lorentz ether theory when
applied to
the moving interferometer might lead to the mirrors not reflecting
light
according to the standard laws of reflection. Sir
Oliver Lodge[1] argued in favour of
Lorentz’s explanation, by referring to the effect of the
Fitzgerald-Lorentz contraction
on the apparatus in preserving the angles and optical path lengths.
This issue
was addressed in detail by Herbert
Ives in 1937,[2]
who argued that “The Fitzgerald-Lorentz contraction may be considered a
means
of introducing a tilt of the inclined mirror just sufficient to correct
this error
and bring the two emergent pulses into coincidence.” If the Lorentz
contraction
is not considered, then an “error of reflection” on the order of ½
v^2/c^2
arises, a term Ives attributes to Lodge. I would like to discuss herein
the arguments
used by Ives to explain why no second order terrestrial aberration
arises in
the moving Michelson interferometer. Explanation: Let’s consider a simple
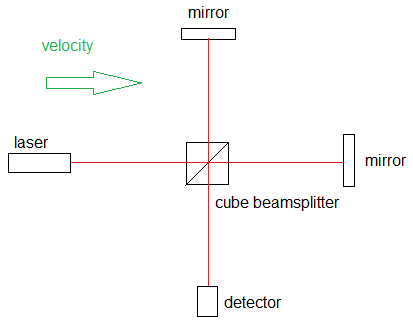
Michelson interferometer as shown in
Fig. 1: Fig. 1:
The velocity is left to right.
Let’s consider the situation where
the velocity is at ½ the speed of light, i.e. v
= 0.5C: From
the time of emission to the
time that the light reaches the beam splitter and mirrors, the optical
components have moved to the right at 0.5C The beam splitter mirror at
45
degrees does not reflect the beam perpendicular as shown but must
reflect the beam
at a forward angle to meet the upper mirror at its new position. The
ultimate
reflection is at a virtual 60 degrees from vertical rather than 45 due
to the
composition of velocities, using the law of Sines. This is shown below
in Fig
2. Fig.
2: 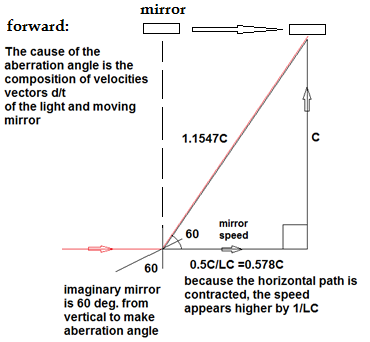
In
the case of the return beam,
the light is reflected at more of an angle backwards due to the forward
motion
of the beamsplitter mirror. In the return case the virtual mirror
appears as if
it is at an angle of 30 degrees to the vertical due to aberration as
shown in
Fig. 3. Fig.
3: 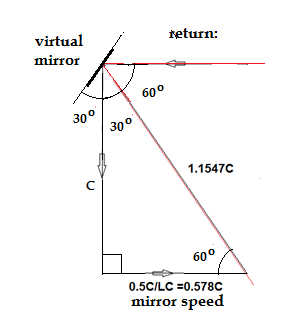
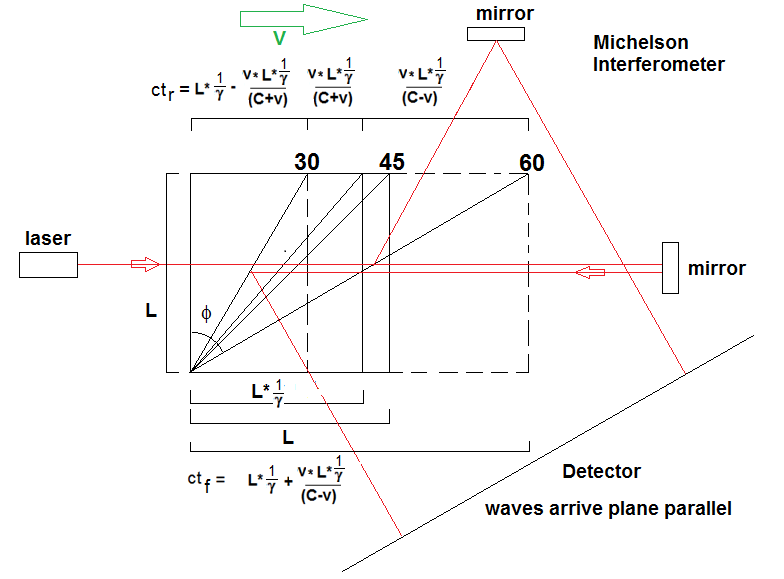
Putting
it all together, the interferometer stretched in velocity is shown
below in
Fig. 4: Fig.
4:
As
is shown in Fig. 4, the
Lorentz contraction, denoted as 1/g,
is
included in the calculation both for the contraction of the length of
the
parallel path due to the motion, as well as the tilt of the
beamsplitter due to
the contraction. Both of these effects add to the aberration angle to
insure
that the return beams arrive at the detector perfectly parallel. If the
Lorentz
contraction is neglected, then a significant angle error will appear
that is
obvious at high velocities. The necessity of requiring a physical
Lorentz
contraction to make the beams arrive at the detector straight (as
occurs in
reality) suggests that the original idea of Fitzgerald, Lorentz and
Larmor
about the contraction of moving matter is valid and not just an ad hoc
hypothesis. This idea was verified by Herbert Ives in his paper “A
graphical
Exposition of the Michelson Morley Experiment.” (1937). Using Ives
calculation method: I
have created a simulator to
demonstrate this effect, click
here to open the simulator. This uses a
modification of Herbert
Ives method to calculate the virtual angle of the moving beam
splitter
mirror to the vertical, and thereby the angles at which the beams
arrive at the
detector. The expected angle f
for the
beamsplitter mirror seen by either the forward or return beam is worked
out by
using the Law of Sines, knowing the virtual lengths of the stretch or
contracted beamsplitter cube based on the values L and ctf or
ctr as
shown in fig. 4. angle f
= ACOS (L/SQRT(ct^2+L^2)) For the forward condition
(Lorentz contraction included,
yes/no = 0): Use ctf
in equation.
angle
f
= 60 degrees when 1/g
= 0.866 (equation
is shown in Fig.4) For the reverse condition
(Lorentz contraction included,
yes/no = 0): Use
ctr
in equation.
angle
f =
30 degrees when 1/g
= 0.866 (equation is shown in Fig. 4) In viewing the above diagram,
60 and 30 degrees respectively
results in the two beams reaching the detector plane parallel when the
Lorentz
contraction of the beamsplitter and path lengths are accounted for. In the simulator, the Lorentz
contraction can be added or
removed to see the difference in the result. If 1/g is set to yes/no
=1 in the simulator instead (no Lorentz
contraction) then: ctf
= 63.435 degrees Ctr = 33.690 degrees Thus
without the Lorentz contraction
of both the length and the resultant twist in the mirror angle, the
beams will
not return rectilinearly to the detector in the Michelson
interferometer. The
angles should diverge from each other by 7.125 degrees. Discussion and
Conclusions
This exercise hopefully demonstrates that not only
is a physical Lorentz
contraction necessary to explain the lack of fringe shift, it is also
necessary
to explain the lack of beam divergence at the detector due to our
motion though
space. This issue was also addressed in detail by Gjurchinovski
(2004) in a detailed analysis
of the reflection of light from moving mirrors. He states: “A
common interpretation of the
effect of Lorentz contraction is that relativistic contraction is not a
real,
physical contraction, but an apparent, artificial phenomenon, whose
presence is
solely due to the process of relativistic measurement of the
length…however, we
showed that Lorentz contraction is a real effect and is an inherent
physical
property of a mirror (and, therefore, of any object) in uniform
rectilinear motion.
As a physical property of an object in motion, Lorentz contraction is
not just
a result of the process of relativistic measurement of the object’s
length.” [4] In
this regard, Gjurchinovski
[4] appears to concur
with Ives that the Fitzgerald-Lorentz contraction is a real, physical
contraction of the optical apparatus, and that the relativistic
interpretation
of the Lorentz contraction does not fit the data. References: [1]
Sir Oliver Lodge, The Ether
of Space (1909) Harper Brothers, P. 140. [2]
Herbert Ives, “Graphical
Exposition of
the Michelson Morley Experiment”. Optical Soc. Am. Vo. 27 No.
5 1937. P.177
– 180. [3]
Janssen, Michael,
http://www.mpiwg-berlin.mpg.de/litserv/diss/janssen_diss/Chapter3.pdf [4]
Aleksandar
Gjurchinovski, “Reflection
of light from a uniformly moving
mirror.”
Am. J. Phys.
72 (10), October
2004. |