|
The Use of Moved Clocks:
How this challenges Special Relativity:
D.M.
Marett (2010)
Einstein's
special relativity has as one of it's primary tenants that the speed of
light is exactly C for all inertial observers. Herein
I explore a
thought experiment which demonstrates that if
one uses synchronized
clocks and meter sticks to measure the speed of light in one direction,
and then back, that the speed of light has to be different in the two
directions for at least one inertial
observer. This requires making
some assumptions that are not much of a stretch - you need to be able
to synchronize clocks (already done in GPS), and you need to
be able to
define which observer is moving faster. We also need to ignore the
Einstein clock synchronization method usually used in special
relativity (SR). One of the big problems with the theory of relativity
has to do with how it synchronizes clocks. According to Einstein’s
method, the speed of light is defined by measuring the time for a two
way propagation of light to proceed from one clock to a distance mirror
and back. But
what if C is not the same in both directions? Relativity
assumes it to be so a priori. Our
thought experiment is designed to settle the
issue by looking at the
predictions made by any medium of space theory where there is a
preferred frame for light, and comparing this to predictions made by SR
where the speed of light is supposed to be constant for all
inertial
observers.
To
perform such a test, first we establish how we will synchronize our
clocks. We take two clocks, synchronized immediately next to one
another by some electromagnetic means. We then move one at a velocity v
= 10m/s to 1000m away ( takes 100 seconds). This clock has then slowed
by:
100 s x
(1-v^2/c^2)^1/2 – 100 = 1/2t*v^2/c^2 = 5.55555555555555709876543209 E
-14 seconds [4]
If this amount is then added to the moved clock, then the two clocks
can be considered synchronized, as long as the two clocks remain in a
fixed position relative to one another in the same moving frame.
Following this procedure the one way speed of light can be
measured.
When light leaves the first clock, the time is marked. When light
reaches the second clock, the time is marked. The difference in the two
readings is the elapsed time. Similarly, if the same procedure is
performed in the opposite direction, then the time of flight back can
also be independently calculated. According to the theory of
relativity, Cf = Cr = C. We
begin by asking
what would be the predicted result if there is a preferred frame for
light in space vs. no preferred frame (SR) if these two clocks
are on
the translating Earth in its orbit around the Sun at 30 Km/s:
From the Preferred
Frame Perspective:
For the Forward Path:
C = 3 E 8 m/s
V = - 3 E 4 m/s
C + V = 2.9997 E 8 t m = 1000 m
t =3.3336666 E -6 s
(velocity is negative, since C is being slowed by
media)
For the Reverse Path:
C = 3 E 8 m/s V = 3 E 4 m/s C + V = 3.0003 E
8 t m = 1000 m
t = 3.3330000
E -6 s
(velocity is positive,
since C is travelling with media)
The total time
difference is: 3.3330000E
-6 s
+ 3.3336666E -6 s =
6.6666667 E-6 s
From the Relativity Perspective:
For the Forward Path:
C
= 3 E 8 m/s V = 0 C + V = 3 E 8 t
m = 1000 m t
=3.3333333 E -6 s
For the Reverse Path:
C = 3 E 8 m/s V = 0
C + V = 3 E 8 t m = 1000 m
t = 3.3333333
E -6 s
The
total time difference is: 3.3333333E
-6 s
+ 3.3333333E -6 s =
6.6666667 E-6 s
The
two perspectives agree on the arrival time of the light back at the
first clock, but they disagree on the one-way travel times, since if
space is a preferred frame, one would need to add and subtract the
velocity of the Earth from that of the light, whereas if relativity is
correct, then the speed of light does not change. If we look at the
preferred frame scenario, the synchronized clocks on Earth show two
different one-way propagation speeds, but if the clocks were in space
at rest in the preferred frame instead, then we would see the speed of
light as constant (c) in both directions, and we would expect
the paths
to be measured as different lengths. Lets now perform a second
thought
experiment, this time using clocks that are all synchronized, both in
space and also on the Earth as shown in Figure 1:
Fig. 1:
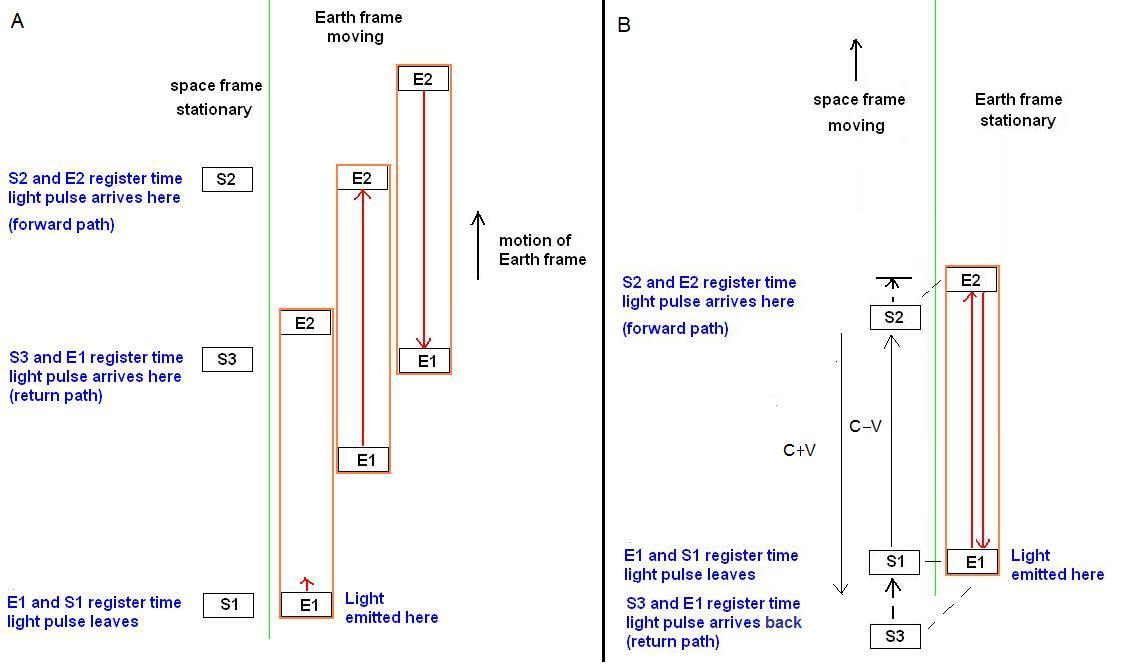
Referring
to Fig. 1A, for clocks in space, these are synchronized to each other
by the method described above, and adjusted
to Earth time (Earth time
will be our standard) by slowing them down by (1-v2/c2)1/2
to account for the velocity of Earth. The Earth
clocks are also
synchronized and counting in Earth time.
The space
clock S1 is positioned to be directly beside the Earth clock E1
when Earth passes by S1 in its orbit, and starts at
the same time as
when the beam of light leaves E1. Synchronization is not a problem
because they are side by side at that moment (verified by
contact). The space
clock S2 is at the exact position where the mirror will be on the Earth
(at clock E2) when the light beam on Earth reaches it and is triggered
at the same time because at that moment they are also side by
side. Finally, clock
S3, synchronized with the first two, is at the exact position
where clock E1 on Earth will be when the return light
beam arrives.
It
might be considered a problem coordinating the positions of the space
clocks to match those of the Earth clocks - to remidy this, we could
think of space as having a line of consecutive synchronized clocks, and
the clocks that are triggered are the ones that are in the correct
position when the light reaches each Earth clock.
A
common standard of length is used - a meter stick on Earth. If two
clocks on Earth are 1000 Earth meters apart, then the two corresponding
clocks in space will be 1000 Earth meters apart, since they trigger
only when they are in the same space at the same time. Therefore there
is simultaneity of both length and time. We are not concerned that the
length of the Earth meter may appear to be longer (relativity) or may
actually be longer (Lorentz theory) in the space frame, - if we want to
switch reference lengths we can easily do this
by adjusting the meter
length by the factor 1/(1-v2/c2)1/2
when it is moved from the Earth
to space.
The
important point is that the spaces clocks are in exactly the same place
at the same time as the Earth clocks when they meet the beam, so that
we can be sure that the lengths between them are perfectly correlated,
regardless of which meter stick we use to measure with.
We
then measure the forward and return speed of light on a two way path
(1000m each way) on Earth, from the perspective of
clocks synchronized
to a common time (Earth time) both on Earth and in space. The predicted
results of the two scenarios (preferred frame, SR) are shown below:
Table
1: On Earth Prediction: Space is preferred frame, Earth is
moving at V with respect to it.
|
Beam Direction:
|
Speed of light (C)
|
Velocity of Earth
Frame (V)
|
C+V
|
Distance (D)
|
total Earth time (t)
on Earth Clocks
|
|
Earth Forward
|
3 E 8 m/s
|
- 3 E 4 m/s
|
2.9997 E 8 m/s
|
1000 m
|
3.3336666 E-6 s
|
|
Earth Reverse
|
3 E 8 m/s
|
+ 3 E 4 m/s
|
3.0003 E 8 m/s
|
1000 m
|
3.3330000 E-6 s
|
The total Earth time
difference forward and reverse is : 3.3330000E -6 s + 3.3336666E -6 s = 6.6666667 E-6 s
Table 2: In Space Prediction: Space is preferred
frame, Earth is moving at V with respect to it.
|
Beam Direction:
|
Speed of light (C)
|
Velocity of Space
Frame (V)
|
C+V
|
Distance (D)
|
total Earth time (t)
on Space
Clocks
|
|
Earth Forward
|
3 E 8 m/s
|
0
|
3.0000 E 8 m/s
|
1000.1 m
|
3.3336666 E-6 s
|
|
Earth Reverse
|
3 E 8 m/s
|
0
|
3.0000 E 8 m/s
|
999.9 m
|
3.3330000 E-6 s
|
The
total Space time difference forward and reverse is: 3.3330000E -6 s + 3.3336666E -6 s = 6.6666667 E-6 s
Table 3: Earth or Space
Prediction of Special Relativity: Earth V
has no effect on C.
|
Beam Direction:
|
Speed of light (C)
|
Velocity
of Earth Frame (V)
|
C+V
|
Distance (D)
|
total Earth time (t)
on Earth/Space
Clocks
|
|
Earth Forward
|
3 E 8 m/s
|
no effect on C
|
3.0000 E 8 m/s
|
1000 m
|
3.3333333 E-6 s
|
|
Earth Reverse
|
3 E 8 m/s
|
no effect on C
|
3.0000 E 8 m/s
|
1000 m
|
3.3333333 E-6 s
|
The
total Earth / space time difference forward and reverse is : 3.3333333E -6 s + 3.3333333E -6 s = 6.6666667 E-6 s
What
is happening with the space clocks:
Space
Clocks: Earth Forward Path:
C
= 3 E 8 m/s V
= 0 C+ V = 1000.1 meters t = 3.3336666
E-6 s (Earth
clock)
t = 3.3340000 E-6 s (uncorrected
space clock)
t = 3.3336666 E-6 s
(corrected space clock)
Since
the Earth frame is moving - clock E2 has moved 0.1 meters with respect
to space when it is triggered, which is added to the space length
measured.
Space Clocks: Earth
Reverse Path:
C = 3 E 8 m/s
V = 0 C+
V = 999.9 meters t
= 3.3330000E-6 s
(Earth clock)
t = 3.3333333E-6 s
(uncorrected space clock)
t = 3.3330000E-6 s
(corrected space clock)
Since
the Earth frame is moving - clock E3 has now moved 0.2 meters with
respect to space when it is triggered. This is subtracted from
the
first 1000.1 meters to get 999.9 meters as the length measured in
space.
Space clocks display absolute Earth
time, slowed down from uncorrected space time
by the factor: (1-v2/c2)1/2.
Earth clocks display Earth time, and can display
uncorrected space time if they are sped
up by 1/(1-v2/c2)1/2.
Uncorrected space time round
trip:
t = 3.334000 E-6 s +
3.33333333E-6 s = 6.667333 E -6 s
Corrected space
time/Earth time round
trip: t = 3.33366 E-6 s + 3.3330000 E–6
s = 6.66666667 E -6 s
We
find that mathematically, if the clocks are all reading at an identical
rate, and they trigger at an identical time, then the one way speed of
light must be C-V in the forward direction, and C+V in the return
direction. If this were not true, then the Earth could not be moving
relative to space clocks. The only situation that would agree with SR
under these conditions is if there was no relative movement. We then
take as our correct result below:
Table 1: Speed of Light (Earth Observer): = C+V,
C-V, distance is 1000 meters both ways
Table 2: Speed of Light (Space Observer): = C both
ways, distance is 1000.1 m and 999.9 meters.
In considering Fig. 1A, the
Earth time and space time that has elapsed (corrected to Earth
time) agree on the one-way
elapsed time for the preferred frame model, but not the Relativity
model. We find that they agree because the speed of light is
different
in the two directions for an Earth observer but the distance is the
same, but for a space observer it is the reverse, the
speed of light is
the same in the different directions but the
distance is different.
When one then uncorrects the space clock to count in the actual time
that it would display on its face, one gets a
longer elapsed time.
According to this time, the speed of light is no longer C in space, but
2.9997E8 m/s on average. We arrive at a situation similar to that of
the Sagnac interferometer - one observer (on the axis) sees the speed
of light as constant and the distance different in each
direction, the
other observer (on the rim) sees the distance as the same, but the
speed of light different in each direction. Correcting the clocks to
one another does not change this relationship, nor does correcting
for the length viewed in Earth meters vs.
space meters. The ultimate
result of using a synchronized time and a synchronized length is that
the speed of light must by definition be C+V and C-V in at least one of
the frames, contradicting the postulate of relativity that the speed of
light is constant for all inertial observers. This is
why relativity must use the Einstein time synchronization
method
and suggests that clocks in different inertial frames can't be
synchronized, since otherwise we lead to this (real)
contradiction (1).
The only requirement to get to this result is that we need to know to
begin with which way to calibrate the moving clocks, i.e. is space
moving slower that the Earth, or is it moving faster. In most
situations this is definable - the Earth's orbital frame is
moving
faster than the Sun (heliocentric) frame, the Earths diurnal
rotation
frame (ECEF) is moving faster than the frame of the Earth's pole (ECI
frame), etc. And ultimately, the relative velocity of objects can be
referenced to the Cosmic Microwave Background, which appears to be a
true rest frame for the universe.
Is
this just an artifact of picking the Earth as the moving frame? If we
look at the next simulation in Fig. 1B,
where we reverse things and
have space moving hypothetically and the Earth is at rest, we
arrive at
a similar result. On Earth the speed of light is measured as 3 E 8 m/s
in both directions, and the distance is measured to be 1000 meters
using the Earth meter. In space, the distances measured and the speeds
of light in either direction now become C-V and C+V:
Table 4: On Earth Prediction: Earth
is a preferred frame, Space is moving at V with
respect to it.
|
Beam Direction:
|
Speed of light (C)
|
Velocity of Earth
Frame (V)
|
C+V
|
Distance (D)
|
total Earth time (t)
on Earth Clocks
|
|
Earth Forward
|
3 E 8 m/s
|
0 m/s
|
3 E 8 m/s
|
1000 m
|
3.3333333 E-6 s
|
|
Earth Reverse
|
3 E 8 m/s
|
0 m/s
|
3 E 8 m/s
|
1000 m
|
3.3333333 E-6 s
|
The total Earth time
difference forward and reverse is : 3.3333333E -6 s + 3.3333333E -6 s = 6.6666667 E-6 s
Table 5: In Space Prediction: Earth is preferred
frame, space is moving at V with respect to it.
|
Beam Direction:
|
Speed of light (C)
|
Velocity of Space
Frame (V)
|
C+V
|
Distance (D)
|
total Earth time (t)
on Space
Clocks
|
|
Earth Forward
|
3 E 8 m/s
|
-3 E 4 m/s
|
2.9997 E 8 m/s
|
999.9 m
|
3.3333333 E-6 s
|
|
Earth Reverse
|
3 E 8 m/s
|
+ 3 e 4 m/s
|
3.0003 E 8 m/s
|
1000.1 m
|
3.3333333 E-6 s
|
The total Earth
time difference forward and reverse is : 3.3333333E -6 s + 3.3333333E -6 s = 6.6666667 E-6 s
The frame that is moving faster is consistently the one where
the speed
of light doesn't equal C in either direction once all clocks
and
lengths are synchronized.
GPS is the first practical system which uses synchronized clocks in
daily practice. Do GPS one-way propagation range times provide any
clarification on this? Yes, it does. The satellite is
in a frame moving
with the Earth in its orbit, and the receiver is in a frame also moving
with the Earth in its orbit as well as rotating diurnally. GPS
range
times suggest that the one-way speed of light is constant in the frame
of the orbiting Earth (ECI frame), but the velocity is C+V and
C-V in
the frame of the rotating Earth (ECEF frame), where V is the Earth's
rotational velocity. Again, two frames, and in one the speed
of light
is not C. This contradiction
was pointed out by Herbert Ives in “Genesis of a Query “Is there an
Ether?” (3) where
Ives says:
“From
the contractions of length and clock rate with motion contained in
these transformations it is possible to determine the Epoch of the
moved clock. When this is done, and time is measured by the moved
clock, the velocity of a one way signal turns out to be a function
involving the moved clock velocity, that is, it is not “c”,
contradicting the initial postulate.”
Conclusion:
This
exercise shows that it is possible to synchronize clocks in two
velocity frames, by moving them in accordance with the corrections due
for velocity and distance, and correcting them for their relative
velocity. When this is performed, the clocks agree that the one way
speed of light adds and subtracts with the velocity of relative
movement between the frames, and uncorrected clocks reading in one
frame or the other will give erroneous and contradictory readings. This
is a consequence of our fore-knowledge of which frame is faster,
information which is usually available to us, as well as our objective
acceptance that relative motion is tangible and measurable. After
synchronization, if we go backward and re-apply all relativistic
corrections to that of a local observer, the difference in the
one way
speeds of light do not go away, since the
corrections affect the one
way speeds of light in an equal manner. If a result
of synchronizing
clocks and lengths in two frames is that the speed of light can be
shown to no longer be constant, then the premise of real time dilation
collapses - this suggests that it is the clocks, and
not actual time,
that are affected by velocity.
References:
1) Tyapkin,
A.A., (1973) "On
the Impossibility of the First-Order Relativity Test."
Lettere Al Nuovo Cimento Vo. 7, No. 15, 760-764.
2) Su, C.
C.,(2001) "A
local-ether model of propagation of electromagnetic wave."
3) Ives,
Herbert, (1953) "Is
there an Ether?"
4) Einstein,
Albert, (1905) "On
the Electrodynamics of Moving Bodies." P.10
|