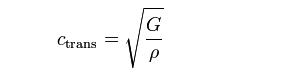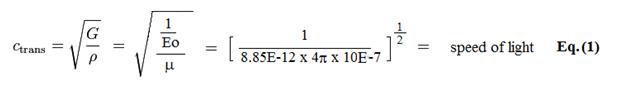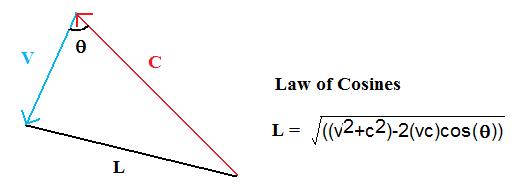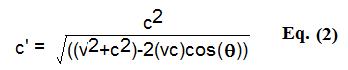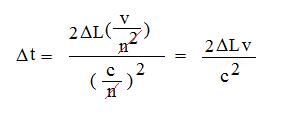The Premise for
Comparing Ether Theories to Relativity Theory copyright 2010 D.M.
Marett
There
is plenty of literature available on how to calculate the
predicted
result of an experiment from a relativistic perspective. However, there
is some confusion about what different ether theories would predict for
the same experiment. Some researchers who believe that there must be a
medium of space, reject ideas like the Fitzgerald-Lorentz
contraction or Larmor
time dilation as being unnecessary. Quite often, they also attempt to
prove their point by suggesting that some experimental results must be
false. Herein the approach is taken that by
and
large the experimental results of the myriad of interferometer tests
and tests on relativity theory are true. Any ether theory that could
possibly describe reality must then be able to predict these same
results in all of these experiments. This is not such a far-fetched
idea, since if we examine the history of the development of relativity
theory, we realize that the theory borrowed many ideas from ether
theory (i.e. the work of Maxwell,
Lorentz
and Larmor) but put them in a slightly different mathematical form.
Because they are so closely related, ether theory usually predicts the
same result as relativity theory for most experiments. To highlight
this idea, I quote from relativist A.A.
Tyapkin from his 1973 paper "On
the Impossibility of the First-Order Relativity Test", "One of the first theoretical explanations for the failure to discover the "ether wind" developed by LORENTZ in a sufficiently complete form in 1904 was in fact, only another way of describing the relativity theory differing from the later one only by the acceptation of the agreement on a single simultaneity of events for two reference systems being in a state of relative motion. As is known Lorentz's approach to the explanation of the negative result of Michelson's experiment retains the presentation of the difference of the velocities of light along an opposite reference system motion, while the impossibility to observe the absolute motion appears as a result of taking into account the effect of the second order of the relativistic contraction of space cuts. It is important to clear out that Lorentz's approach not only should be acceptable for explaining Michelson's experiment, but also should be a consistent system for describing relativity effects for any possible experiments. Many scientists have stated quite justifiably the absence of an "experimentum crusis" for Lorentz theory and special relativity." [1]
It is precisely because relativity theory retained
the ideas of Lorentz contraction and Larmor time dilation from Lorentz
Ether theory (although with a different meaning), that
relativity theory arrives at the same prediction as ether theory for
the same experiment. Likewise, any new or modified ether theory needs
to retain these ideas to be consistent with the experimental results.
An example is the Ives
and Stillwell experiment [2]
- the reduction in the frequency of the canal rays from the high speed
protons was proclaimed as being evidence of relativistic time dilation,
conversely Ives
himself stated, rightly so, that
this was instead evidence for Larmor (mechanical) time dilation and a
physical Lorentz contraction based on Lorentz ether theory. The two
theories agree with the results, but for different reasons. To be
consistent with the results, the ether theory requires Lorentz
contraction and mechanical time dilation to be true. An ether theory
without these two effects would be proven to be false by the same
experiment. Tyapkin
goes on to argue that Lorentz's approach could be proven to be
groundless if an experimental comparison of the light velocities in
opposite directions was possible. The opposite is also true -
relativity theory could be proven wrong if such an experiment could be
devised. For relativists, by definition, such an experiment is
impossible due to issues involving the synchronization of clocks at
each end of the path. Relativists then argue that relativity theory is
the theory of choice because it is "more convenient" or more
"self-consistent". It is also has been argued that something which is
impossible to detect by definition, cannot possibly exist. To quote J.P.
Leahy: "Such is the origin of Einstein's statement ``God is slick, but He ain't mean'' It was made in response to a claim in 1927 that a tiny "ether drift" had finally been detected. Einstein rejected this out of hand: to have an ether which was almost undetectable (requiring special relativity to be almost correct), but yet present (undermining the foundation of relativity) seemed absurd to Einstein, and indeed his intuition proved right. But the comment can be taken more generally as an emotionally powerful justification for the central idea of relativity theory: that what cannot be measured, does not exist. God would not be malicious enough to hide an important part of reality in a way that we cannot reach; if no experiment can reveal the true rest frame of the ether, then there is no ether, and no frame of absolute rest. "
From these statements we
can take that relativity theory has never proved that an absolute rest
frame for light (the ether) does not exist - rather, it has declared
that it is by definition impossible to detect, and as such, does not
exist! We do not agree - in the current world where a universal rest frame has been shown to exist (the Cosmic Microwave background (CMB) radiation) which is now used as an astronomical reference frame for the motion of all objects in the universe, and where clock synchronization has been shown to be possible (i.e. with GPS satellites), it is becoming more and more possible to distinguish between the two theories, and relativity theory, now over 100 years old, is becoming increasingly pressed in its own defence. Further, the idea that because something cannot be measured it does not exist, is an arbitrary scientific justification. Quantum Electrodynamics uses the opposite idea - that virtual particles can exist because their existence is too fleeting to detect due to Heisenberg's uncertainty principle (these virtual particles can also break the law of conservation of energy for the same reason), or the similar idea that particles are composed of quarks even though it is impossible to isolate a quark - this concept in physics is applied in a contradictory and inconsistent fashion as justification for whatever theory is in vogue, and is undermining the credibility of physics as a whole.
It is precisely because of this that we
feel current theoretical physics is going in the wrong
direction, it is
approximating the truth mathematically but failing to describe physical
reality in a deterministic form. We reject the notion that an
experiment is impossible, but
rather accept that it is difficult.
With sufficient progress in technology, theories once believed to be
outside the realm of practical testing will surely succumb to
experimental rigor. Theories obeying the Lorentz
transformations (ether theories, relativity
theory) should be experimentally distinguishable and capable
of being proven true or false.
But
to begin this task, we must first understand how ether theory can be
consistent with all the experimental evidence to
date. We will start
with an
explanation of how there could be a medium of space (a preferred
frame for
light) and light would still appear to be C to all inertial observers.
This explanation is largely based on effects that were well described
immediately prior to the advent of relativity, such as the
Fitzgerald-Lorentz contraction and the Larmor time dilation effects. 1) Explanation
of why the speed of light is the velocity that it is: We start with the
idea that space is a medium of some kind. This was James
Clerk Maxwell's basic assumption when he theorized that
light and electromagnetic waves are the same thing, waves in a medium
of space. Let's look at a simple equation describing the velocity of sound in a medium capable of supporting transverse waves:
where Ctrans
is the velocity of sound in the medium, and G is the shear modulus, and r is the density. This
is identical to the equation referred to by Maxwell in describing space
(Maxwell calls shear modulus the "coefficient of transverse elasticity"
- See James Clerk Maxwell "On
the Physical Lines of Force." P. 499. ) Maxwell found that the magnetic permeability of free space (u) was equivalent to the density of this medium r, and the shear modulus G was equivalent to the reciprocal of the electric permittivity of space (Eo).
It follows then that
the speed of light has a specific
velocity because this is the velocity of transverse waves in the medium
of space, and this velocity is a function of the elasticity and density
of this medium. Conversely, if space was a true vacuum, there would be
no specific velocity attributed to light, since the only property of
emptiness is that it has no properties.
2) If light is a
transverse wave in a medium, how do we calculate the speed of light
with respect to a moving observer? If
we were to imagine that we the observer are immersed in this medium,
and light waves are waves in this medium, and we start to move at some
velocity, what would the speed of light be with respect to us? We start with the simple addition of velocities:
If
light is moving at velocity C with respect to the medium (the page) and
I am moving at velocity A also with respect to the medium, then the
velocity of light with respect to me is simply C- A ( the difference).
Similarly, if I am moving in the opposite direction at velocity B, then
the difference is now C+B. This works well when all relative velocity vectors are parallel, however, when they are not, we must use a triangle diagram and the Law of Sines or the Law of Cosines to work out the final velocity. We place the vectors head to tail with the angle between them being q. By the law of cosines:
Now
C, V and L correspond to the time taken to cover each path. Since V
points against C by a small angle, the time to traverse L is less than
the time to traverse C. From the perspective of the
observer moving along V, since the time L is less,
then the observed velocity of light is more than C. To derive the
resultant velocity of light then with respect to the observer, we use
the equation:
Where
C' is the resultant perceived velocity of light with respect to the
observer moving through the medium at velocity V and angle q with respect to the
light. The law of cosines is built into this equation. Lets calculate
some examples: Example 1: The
observer and a laser are on the Earth. The laser is pointing south. If
the observer runs with the laser west at 3m/s, what is the velocity
(C') of the beam of light with respect to the observer? The angle q between the beam and
the velocity of the runner is 90 degrees. v=3 m/s, c
= 3E8 m/s Using Eq. 2 and
plugging in the values:
C' =
299999999.999999985 m/s. One
would imagine that if the measured velocity of light as seen by a
moving transverse observer was less than C, then it should be possible
to detect ones motion. However, as pointed out in "Time Dilation - and
how it could be an Illusion." the clock of the runner (time') will mechanically
slow by exactly the same amount, so the forward and return time of the
light will be measured to be exactly C. This is shown in example 2: Example 2: time'
= time x (1-v2/c2)1/2
= 1 x [1- 32/(3E8)2 ]1/2
= 0.99999999999999995 seconds. c' / time' = 299999999.999999985/
0.99999999999999995 =
300000000 m/s After accounting for
the slowing of the clock, the velocity is now seen as exactly C. This
mechanical slowing of the clock is a conspiracy
of light - it
is a self-correcting process of light where the obvious change in the
apparent velocity of light due to the transverse velocity of the
observer is perfectly cancelled by a change in the speed of light in
the clock of the observer, due to it moving at the same velocity. This
was recognized early on by Joseph Lamor (1897). Example 3: The
observer and a laser are on a plane. The laser is pointing west. If the
observer flies with the laser in a plane west at 300m/s, what is the
expected velocity (C') of the beam of light over the path from the back
of the plane to a mirror at the front? v= -300 m/s, (since
he is flying in the same direction as the beam) c = 3E8 m/s angle q = 0 degrees Using Eq. 2 and
plugging in the values: C' = 299999700.0000000 m/s The time is longer
since the mirror is receding from the beam, so the velocity appears to
be slower. If the beam is sent
from the mirror to the back of the plane, then C'
= 300000300.0000000 m/s since less time has
elapsed due to the observer approaching the oncoming beam. Thus the one way
velocity of light appears to be C+/- v, depending on which was he
flies. However,
our observer can't actually measure the time it takes for light to
cover the distance from start to finish, since he is at the back. The
only way he can do that is to reflect the light from the mirror at the
front end of the plane and measure the two way trip. In this case, the
velocity is: (299999700.000 + 300000300.000)/2 = 300000000.000 m/s The average velocity
is C. This is a conspiracy
of light (first order) in
that although the one way speed of light is not C, the two way speed of
light averages to C since the observer cannot be at the front and back
at the same time. However, if we look
at the time in detail for the round trip, (with L = 1 m) it is
actually: t = L/(c-v) +
L/(c+v) = 0.000000006666666666673330 seconds
( plane is moving at 300m/s) which differs from 2L/c = 0.000000006666666666666670 seconds
(plane is not moving) The time is a little
longer so the speed of light measured is slower by: C' = 0.9999999999990 x C = 299999999.99970
m/s (A) This small difference should be detectable, just like in example 2. However, two effects come in to play to obscure this small difference:
1) mechanical
time dilation . Since the observer is flying at 300m/s his
clock runs mechanically slower by: time x (1-v2/c2)1/2
= 0.99999999999999995 seconds So he should measure
the 2 way speed of light as actually C' = 299999999.999700 m/s / 0.9999999999995 s = 299999999.99985 m/s (B)
2) The Lorentz
contraction. With the Lorentz
contraction, the length of the path is also contracted by: L x (1-v2/c2)1/2
= 0.9999999999995
x L
Thus the measured
speed of light is further corrected from (B) by: 299999999.99985 m/s / 0.9999999999995 = 300000000.00000 m/s
Thus the two way measured speed of light is C, the difference being obscured by two conspiracies of light: 1) the mechanical time dilation and 2) the Lorentz length contraction, both second order effects. The Equations of
H.E. Wilhelm: H.E. Wilhelm [3] wrote a paper in 1992 (Aiperon) that attempted to explain the results of two famous historical experiments on the propagation of light: The Fizeau experiment (1851) and the Hoek experiment (1868). The thing that was important about these two experiments is that they attempted to use dielectric media with a refractive index > 1 to affect the propagation velocity of light and thereby make ether drift visible in the experiment. The set of equations used by H.E. Wilhelm are derivable from Lorentz's theorem of corresponding states. In 1892 Lorentz wrote an extensive treatise on the electrodynamics of moving bodies, and was able to show that for a wave propagating along the direction of motion of a frame moving with velocity v, must have a velocity c/n - v/ n2 in that frame (to order v/c). Hence, the wave velocity with respect to the ether would be c/n - v/ n2 + v = c/n + v (1-1/ n2) in accordance with the Fresnel coefficient. This new view of Lorentz suggested that it is the waves that are partially dragged and not the ether. The electric field of the wave displaces the electrons in the refractive medium creating a common motion. The moving electrons are then subjected to an additional Lorentz force from the magnetic field of the wave. Both of these effects reduce the velocity of the wave by v/ n2 from the value of c/n when the medium is at rest in the ether (5). Wilhelm devised the following equation to explain both the experiments of Fizeau and Hoek by calculating the Doppler shifted phase velocity in a
moving (v) dielectric (i.e. Fizeau) with ether velocity (w) (i.e.
Hoek): Generalized Wilhelm Equation: The
important thing about this equation is that it provides a method of
calculating the final velocity of the light in a media with a
refractive index >1 including the velocity of the ether drift.
These
velocities do not simply add and subtract in a Galilean fashion when
R.I .> 1. In glass for example, the measured speed of light C'
with
an ether wind v would be: C' = c/n +/- v/n2, where n = 1.47 rather than C' =( c +/- v) / n
If the dielectric
media is moving rather than the ether frame, the equation becomes: C' = c/n + ( 1-1/ n2 )v ,
where v is the
velocity of the dielectric. This is latter
expression is essentially the equation that Fizeau had worked out. Wilhelm combined these two equations together into an equation to calculate the velocity of light in any path of an interferometer (Eq. 3) or the propagation time of light in any path of an interferometer (Eq. 4). However, the Wilhelm equation uses simply the cos of the angle between the velocities as a factor, which is inaccurate at second order. To explain, if we return to example 1 above, Wilhelm's equation would give us V = c + wcosf/n2. Since the angle is 90 degrees, and the refractive index n = 1, and the velocity w = 3m/s,
the equation reduces to
V = c + 3*(0)/1 = c. As can be seen, the effect of the transverse
velocity of the observer (i.e. when the observer is moving
perpendicular to the light beam direction) does not figure in the
Wilhelm equation, which would be C - 1.5 E -8 m/s, a very small second
order difference, but very relevant in sensitive optical experiments
such as the Michelson and Morley experiment. Nor is the counteracting
effect of mechanical time dilation taken into account. Further, when
the velocity of the observer and the beam of light are parallel, wcosf = w (since cosf
=1) and if we were to simply average the velocities forward and back
along the path L, we would get an average velocity of C and would not
see the small second order time difference shown in example 3 that
leads to the round trip velocity of light being 299999999.99970 m/s
rather than C.
We
therefore modify the equation as follows by adding in the law of
cosines equation developed in Eq. 2. Further, we must calculate the
result in terms of propagation time along the path rather than by
calculating the velocity along the path, since we cannot simply average
the velocities without taking into account that the effective path L is
different from the perspective of the light beam fixed to the medium. Our generalized propagation time equation for a light beam as measured by an observer is:
The sign of the
velocity (v) depends
on whether the velocity is that of the observer, or that of the
apparent ether wind and the observer is taken to be stationary. The
effect of mechanical time dilation is not part of this equation, and is
applied later as required. For interferometer experiments where we are
looking only at the phase difference between different beams of light,
mechanical time dilation cancels in the result since both beams are
observed in the same velocity frame at the detector. The equation simplifies to:
for most
interferometer experiments excluding the Fizeau experiment. The idea of using the relation C' = c/n +/- v/n2 is also consistent with Sagnac interferometers. The classic Sagnac equation: Dt = 4Aw
= 2(pi)r * 2v
c2 c2 can be re-expressed
in the equation used by Ruyong
Wang [4] to describe the Sagnac interferometer: Dt =
2vDL/c2. Wang points out that: "The travel time difference Dt = 2vDL/c2 in our experiment is independent of the refractive index n, as in the Sagnac type experiment." This makes sense if c/n +/- v/n2 is added in as below:
This is because n2 cancels out in the numerator and denominator, making the Sagnac device independent of refractive index n. Conclusions:
We have developed a generalized equation (Eq. 5, Eq. 6) that can be
used to calculate the propagation time and velocity for a beam of light
in any arm of an interferometer, on the basis that there is at least
one preferred frame of reference for the light (i.e. an ether). The
equation takes into account: 1) refractive index
of the arm, 2) the motion of the
arm with respect to the ether at any angle 3) the motion of the
dielectric of the arm with respect to the apparatus at any angle 4) any Lorentz
contraction of the arm This equation can now be applied to the various experimental results of interferometer test carried out in the last 150 years to see if theories that call for a preferred frame of reference, such as the Lorentz Ether Theory (LET), and Gravitational Frame Dragging Theories (GFD) yield the correct result. The results obtained can then be compared and contrasted to the predictions of relativity theory for the same experiments. This is performed in the next series of papers on this website. References: See: http://conspiracyoflight.com/Historical Papers.html 2) Herbert Ives and G.R. Stillwell (1938) An Experimental Study of the Rate of a Moving Atomic Clock. JOSA 28,No.7, 215-226. 5) Janssen, Michel, Stachel, John, The Optics and Electrodynamics of Moving Bodies. 2004. |