|
Some
Notes on Understanding the Schrodinger Wave Equation
D.M. Marett 2006
Some
Useful Resources:
The
Orbitron - An
excellent website for modelling orbitals
How did Schrodinger
arrive at his wave equation? This is a short mathematical exercise to
get to the root of what the equation is really describing, and how to
go through the math step by step to derive information about the
simplest of the atoms, hydrogen. In order to do
this, we start with an equation to describe a
plane wave moving through space. In 2D, a point at x on the x and y
axis, which has a plane wave moving through it, will oscillate up and
down with the peaks and troughs. The amplitude of x (in units of y)
will then obey the travelling wave equation:
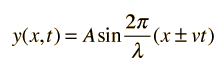
Where for a fixed
position y, as time passes (t changes) for a fixed velocity v, and
maximum amplitude A, the value of y will change sinusoidally reflecting
the up and down movement of point x. See the Wikipedia article here or the Hyperphysics
explanation here for more detail.
Schrodinger knew that de Broglie had described
an
electron as a wave moving around the nucleus. Thus Shrodinger tried to
model what would happen if a wave moved around the nucleus, such as a
travelling wave. He used the equation:
For the point x
independent of time, he used (Ref1):
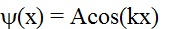
Now, Shrodinger needed to somehow
equate the energy of the electron as a particle, with the energy of a
travelling wave. If he could do this, then he could substitute the
travelling wave equation into Bohr’s equations for the motion of an
electron around the nucleus, and model the particle as a wave.
Shrodinger knew that:
1) The total energy of an electron =
its kinetic energy + its potential energy.
KE + PE = E total
KE = 1/2mv2.
2) That the wavelength he wanted was
the de Broglie wavelength, that could be expressed as:
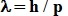where p = momentum
3) The potential energy of an
electron in a hydrogen atom is:
U = kQ
q where: k = coulombs
constant, 9 x 10 9 N
r
Q
is the charge of the electron
q
= charge of the proton
r
= radius
= 13.61eV x 2
To equate the kinetic energy of the
particle to the energy of the wave, Schrodinger had to use an
expression for kinetic energy that included the wavenumber k.
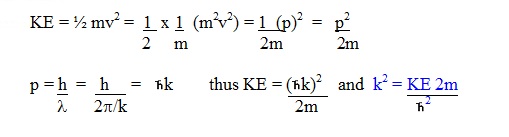
Having written the
kinetic energy of the particle in terms of k, he now had to write the
travelling wave equation in terms of k as well (Ref1).
The travelling wave equation,
independent of time was:
y(x)
=
Acos(kx)
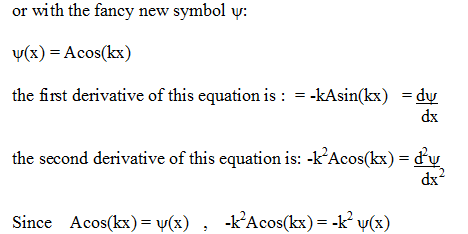
This is just basic
calculus. The use of the second derivative
d2y
in
describing travelling
dx2
waves is also shown
in the Hyperphysics reference here.
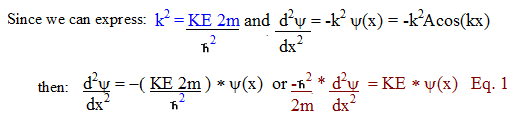
Now
Schrodinger had an equation to express the travelling wave in terms of
the kinetic energy of the electron around the nucleus. However, he
wanted to be able to include the potential energy in the equation,
since this value was usually the only known value.
To do
this, he had to substitute the KE value for a value including the potential
energy U.
KE + U =
E total, thus
KE = E-U
The
constant A is usually determined by evaluating or setting boundary
conditions.
For an
electron and a proton, the U force between them is:
-e2
4peo r
We also need to
determine the second derivative  of the distance r in spherical
coordinates.
This is:
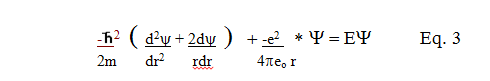
At
Ref1 it
is explained how this equation is then applied to the
situation of a real atom, such as hydrogen:
For the
case of the hydrogen atom: 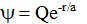 where Q and a are
constants.
The first
derivative of this expression with respect to r is :
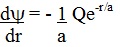
The
second derivative of this expression with respect to r is :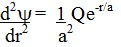 
How the equation for 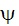 was
determined is not shown.
For the
hydrogen atom, a = 1 Bohr radius and Q =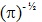 
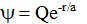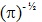= e –r/
5.29E-11m
How
do Imaginary Numbers come into the Schrodinger Equation?
We start with the 1D time independent equation:
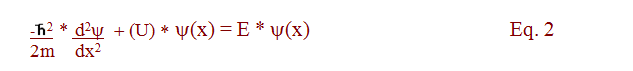
For the time-dependent
form of the equation, it is stated that:
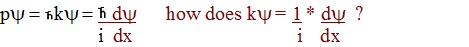
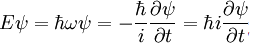
To understand how
imaginary numbers are used to describe waves, we need to understand Euler’s formula and how it
is applied to plane wave equations:
Euler’s Formula:
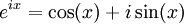
A wave moving in the x-direction has the form (the
general form of the wave function):
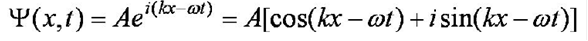
Ref:
http://www.mines.edu/Academic/courses/physics/phgn300/Sarazin/PDFs/QuantumLect4.pdf p.
3.
Basically, one wants to know how the
imaginary number i gets introduced into the Schrodinger
equation. Start with the equality:
py
= hky =
h dy
2p
2p
i
dx
thus:
ky = 1 *
dy
i dx
The obvious question is, how does the i get into
the equation if
y=
ACos(kx)?
After checking the site
http://en.citizendium.org/wiki/Schr%C3%B6dinger_equation, they referenced another site at:
http://walet.phy.umist.ac.uk/QM/LectureNotes/ under "The Schrodinger Equation - the state of the
quantum system" where one finds the equality
used again. And
here is the trick - now, rather than using y=ACos(kx) to describe the planewave (1D), they
use the equivalent expression for a plane wave from Euler’s formula:
Aeix= A[cos(x) +
isin(x)] where x = kx (for 1D) or kx-wt
(for 2D)
Thus
y=Aei(kx)
which describes a plane wave
(1D) as well as y=ACos(kx)
but is complex.
The
derivative of Aei(kx) is:
dy =
ikAei(kx)
dx
Thus
ky
= 1 * dy =
1 * ikAei(kx)
= k * Aei(kx) = ky .
i dx i
So
that is the answer - they use y=ACos(kx)
to develop the first part of the 1D Shrodinger equation, and then when
they want to make the equation time dependent y(x,t),
they introduce complex numbers using the alternative plane wave
expression
y=
Aei(kx-wt).
In
the end, the Schrodinger equation doesn't seem as difficult if one
understands that rather than moving around simple variables to make
things add up, instead they introduce the derivatives of variables to
make them add up. Unfortunately, this leads to a partial differential
equation that is very hard to solve.
Rather than solving the partial
differential equation arising in the 1D Schrodinger equation,
it appears that the answer is usually arrived at by “guessing” that the
the wavefunction corresponds to a form:
.
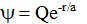This is the associated Laguerre function for 1s hydrogen.
From this guess, one
works backwards. See:
http://spiff.rit.edu/classes/phys314/lectures/sch_hyd/sch_hyd.html
http://www.physics.gatech.edu/gcuo/lectures/ModernPhysicsLectures/MP16HydrogenAtom.ppt#11
http://phy.asu.edu/phy361-alarcon/SPRING07/lecture20_0405.ppt#11
Where it is always
taught the same.
The derivatives of this
associated Laguerre function are then inserted into the equation:
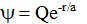
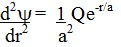which
are
then inserted into equation 3 below:
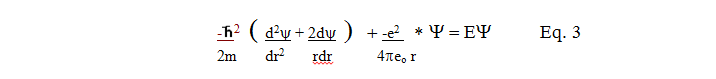
Eq. 3 then becomes:
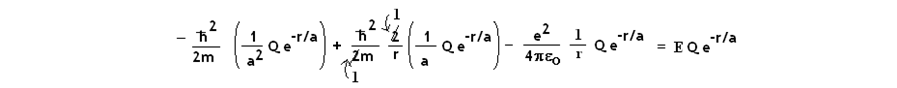
Since two terms contain 1/r * e-r/a
, and two terms contain only e-r/a , for the
equation to work at all values of r, the terms with the same variables
have to equal each other. Thus:
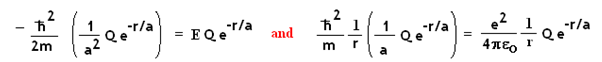
Cancelling out the
common terms on both sides of the equations, a and E are easily solved
for the hydrogen atom:
a =
5.29 E -11 m,
E= 2.18E-18 J (13.61 eV)
****** |
