Gravitational Time Dilation - A Lorentzian Interpretation Doug Marett (2010) (updated April 6th, 2011 and Nov. 5th, 2013) The phenomenon of time dilation is fundamental to Einstein's relativity theory, both Special and General. This is principally because it is the issue of whether time dilation is real or illusionary which set Einstein's theory apart from the Lorentz ether theory immediately preceding it - by staking as the tenets of the theory that the speed of light is constant and everywhere the rate of time is a variable, the consequence is a 4D space-time where "time" becomes the key dimension. Conversely, if Lorentz's theory had been suitably advanced to take into account gravitational effects, the fundamental variable would be the speed of light, and rate of time would be the constant instead. As has been pointed out elsewhere, experimentally, the two approaches are indistinguishable - both theories being "Lorentz invariant", they predict the same experimental outcomes - the preference for one theory over another becomes a matter of personal choice. However, Einstein was the first to apply the Lorentz transformations to accelerated frames and gravitational potentials, with his well know predictions of the gravitational bending of light and gravitational time dilation - it was the confirmation of this former prediction which turned Einstein into the scientific superstar that he became, and relegated Lorentz's theory to the back pages of history. If it had been Lorentz and not Einstein who had made this prediction first, our modern scientific course may have turned out entirely differently. The purpose of this paper is to explore the consequences of applying Lorentz ether theory to gravitational potentials - how does this change the model of space from that of Einstein's? In doing so we attempt to simply the jargon of time dilation, by delineating the singular cause of time dilation, rather than viewing it as a consequence of multiple kinds of motions or field effects.
Time Dilation - One Cause or
Many? Let's start with how time dilation is viewed from the Special Theory vs. the general theory of Einstein: The Clock Hypothesis of Special
Relativity: The clock hypothesis states that the tick rate of a clock when measured in an inertial frame depends only upon its velocity relative to that frame, and is independent of its acceleration or higher derivatives. The clock postulate says that even when the moving clock accelerates, the rate of a reference clock to the accelerated clock depends on the factor g=(1-v2/c2)-1/2. That is, it only depends on v, and does not depend on any derivatives of v, such as acceleration. This means that an accelerating clock will count out its time in such a way that at any one moment, its timing has slowed by a factor that only depends on its current speed; its acceleration has no effect at all. Principle of Equivalence of General
Relativity as applied to Time dilation: Clocks which are far from massive bodies (or at higher gravitational potentials) run faster, and clocks close to massive bodies (or at lower gravitational potentials) run slower. This is because gravitational time dilation is manifested in accelerated frames of reference or, by virtue of the equivalence principle, in the gravitational field of massive objects. It can also be manifested by any other kind of accelerated reference frame such as an accelerating car or elevator. Spinning objects such as the earth are subjected to gravitational time dilation as an effect of their angular momentum. This is supported by the general theory of relativity due to the equivalence principle that states that all accelerated reference frames are physically equivalent to a gravitational field of the same strength. To the casual reader, the Special and General theory might appear to be in contradiction - the special theory says that acceleration has no separate effect on time dilation outside of the velocity of the clock - however, the general theory couches all of the terminology of time dilation in the values of acceleration of the clock. The clock hypothesis needs to be consistent with the principle of equivalence - accelerating observers must experience time dilation, but this is only due to their instantaneous velocity along the path, and their centrifugal, centripetal or gravitational acceleration adds no additional term beyond the velocity terms. How gravitational acceleration can be understood in terms of velocity will be described momentarily. The conjecture that acceleration in and of itself has no effect on time dilation beyond the velocity terms has been confirmed experimentally. Below are examples of the experiments of Bailey and Sherwin: Bailey et al., “Measurements of relativistic time dilation for positive and negative muons in a circular orbit,” Nature 268 (July
28, 1977) pg 301.
Bailey et al., Nuclear Physics B 150
pg 1–79 (1979). They stored muons in a storage ring and measured their lifetime. When combined with measurements of the muon lifetime at rest this becomes a highly relativistic twin scenario (v ~0.9994 c), for which the stored muons are the traveling twin and return to a given point in the lab every few microseconds. Sherwin, “Some Recent Experimental Tests of the 'Clock Paradox'”, Phys. Rev. 129 no. 1 (1960), pg 17. He discusses some Mössbauer experiments that show that the rate of a clock is independent of acceleration (~1016 g) and depends only upon velocity. The reader needs to understand that when Einstein talks about an observer on the surface of the earth experiencing a velocity time dilation of v2/2c2 at the equator as compared to the pole, and then another researcher describes a centripetal time dilation at the equator due to the earth's angular momentum, these two effects are one and the same thing - they are not two separate effects. One example is the NTS-2 satellite discussed by Ashby. It was found that it experiences only gravitational time dilation GM/Rc2, and velocity time dilation v2/2c2. When this latter time dilation is called centripetal, it is just another name for it, it is not two effects! The following is the calculation for the rate difference between the satellite clock and the earth clock: Data for GPS satellite NTS-2 NORAD ID: 10091 Int'l
Code: 1977-053A Perigee:
20,058.2 km Average radii R NTS2 = 26,571 km x 2 pi
= circumference / (718.4 x 60) = velocity Average tangential velocity = 3851.33
m/s Gravitational Time dilation rate GM/Rc2
:
Earth
surface =
6.9612E-10 NTS-2 satellite = 1.6698E-10 Difference: = 5.2915E-10 Velocity time dilation rate v2/2c2 = -8.25E-11 total
rate = 5.2915E-10 - 8.25E-11 = 446.6E-12
fast predicted
When measured over a period of 20 days, the satellite clock was found to be fast by a rate of 442.5 E -12 compared to an earth clock. Thus the anticipated time dilation matches the actual time dilation measured for the NTS-2. Time Dilation at Sea Level: Applying
a model of time dilation to the earth is considerably more complicated.
Einstein in his 1905 article argued that an observer on the
equator would experience more time dilation due to their rotation at v2/2c2,
as compared to an observer at the pole. This has been now shown not to
be true; - the rate of clocks at sea level (or more precisely, on earth's geoid
surface) all count at the same rate all over the globe. The reason for
this is that the two competing time dilation effects, gravitational
time dilation and velocity time dilation, cancel out. The conventional
argument goes that earth is an oblate sphere due to the equator bulging
out from the centrifugal force. Since the pole is closer to the center
than the equator, the pole is at a larger negative gravitational
potential -GM/r, and thus experiences a larger time dilation gh/c2
than the equator. However, since the equator observer is rotating at
the tangential velocity v, they experience a counter-acting velocity
time dilation v2/2c2,
which is sometimes referred to as the centripetal term. The height
effect at the pole is almost twice as large as the velocity effect at
the equator; the argument is then that the distribution of mass in the
earth due to its oblateness creates additional gravitational forces
that serve to balance this out. This last term is the gravitational
quadrupole term. When all three terms are added together, the time
dilation on the geoid is the same rate everywhere on the globe. Our
webapp simulation of this calculation is here
which is our attempt to display the calculations taught by Neil Ashby
in his article Relativity
in the Global Positioning System. The
three effects - Gravitational (1), Quadrupole (2) and Centripetal (3)
are calculated to derive the total coordinate time increment for two
clocks at the latitude 1 and 2 in the simulator. The time loss in ns
per day, as compared to a geocentric clock outside the gravitational
field of the earth, is displayed. The total time difference in ns per
day between the two clocks is also shown, as is the projected
difference in height for the clock (the error) as compared to the ideal
geoid of the earth. In
a more advanced simulation of this same calculation, shown here,
inputs are also provided to raise each clock to a height above sea
level, either in the air or on a mountain, as well as to give them a
velocity with respect to the rotating earth. In this manner the results
of a Hafele and Keating type experiment can be displayed in the lower
rows. It is then
possible to calculate the
anticipated difference in clock rates in ns per day for clocks at
different locations on the globe, which can be entered into the
simulator. The three component time dilation effects are then
displayed, with their totals, to demonstrate that the simulator arrives
at the clock rates predicted by relativity theory. As will be shown
later herein, these same predictions are entirely consistent with
Lorentz ether theory, but are based on an altogether different
interpretation of the nature of space and time. See
also our Hafele and Keating experiment simulation here. This
approach to justifying the constant rate of clocks at sea level using
relativity is not without its critics. Murray in Wireless World
points out that Hafele and Keating
attribute the lack of time dilation differences at sea level to the
notion that "the differences in the surface speed at different
latitudes is cancelled to lowest order by a corresponding effect from
the difference in the surface potential owing to the oblate figure of
the earth." Murray counters that if the
gravitational term gh/c2
is added to the centrifugal term Vc (the cause of earth's oblateness)
then the gravitational potential at sea level becomes a unipotential
surface and then there is no general relativistic effect on time
dilation on the earth period. However, a careful examination of the
papers of Ashby
shows that the gravitational potential is equal on the geoid
(approximate sea level) by taking into account the three above
mentioned factors - the centripetal force due to earth's rotations
(which is one and the same with velocity time dilation due to the
rotational velocity), the quadrupole effect which corrects for the
distribution of earth's mass on the oblate sphere, and the height
effect gh/c2 which
accounts for the difference is the radius at the pole vs. the equator,
also due to earth's oblateness. Since these are all relativistic time
dilation effects, and they all add to cancel out, one must accept that
relativistic effects are involved. The confusion, once again, stems
more from the jargon. The velocity time dilation is renamed as the
"centripetal potential", as if it is a gravitational effect distinct
from the special relativistic effect. This generates confusion to
anyone who has just read Hafele and Keating, where velocity time dilation
and gravitational time dilation are treated as two competing terms.
Centrifugal Force and Time Dilation: The fact that the centrifugal force at the equator does not counter-act the time dilation effect of gravity demonstrates that gravitational acceleration and centrifugal acceleration are not equivalent at all. The former subtracts from the latter to lower the gravitational acceleration, but when it comes to the calculation of time dilation, it is treated as a centripetal force instead, under which the two component effects add to increase the time dilation. This is why what is referred to as "centripetal acceleration" component of time dilation is inappropriately named - it should be called the velocity time dilation effect, since acceleration, in and of itself, has no effect on time dilation beyond its velocity effect. The
Hafele and Keating Experiment The Hafele and Keating experiment was a clock experiment performed in 1971 to test Einstein's predictions regarding the dilation of time in clocks moved at some velocity with respect to a stationary clock. In the opening statement of the first of two papers on the subject, the authors refer to the debate surrounding the "twins paradox" and how an experiment with macroscopic clocks might provide an empirical resolution. In the original "twins paradox" a twin travels in a rocket into space at high speed and then returns to earth sometime later to find that his stay at home twin is older than he is. The paradox arises because according to relativity, motion is relative, then each twin could perceive the other to have travelled, so on return each twin should perceive the other to have aged more slowly. In Hafele and Keating's experiment, they flew caesium clocks around the world in opposite directions near the equator, and then measured how much time they have gained or lost when they return to the start point and are compared to a stationary caesium clock, to which they were originally synchronized. The experiment of Hafele and Keating (HK) actually differs from the twins paradox thought experiment is some important ways - firstly, in the twins paradox, the traveling twin travels in a straight line to a distant point then turns around and comes back, with a series of accelerations and decelerations. In the HK experiment, the journey is circular and the clocks never leave the earth. These details actually make a difference in what Einstein originally predicted and in the interpretation of the final result. In Einstein's paper of 1905 , 1907, and elsewhere, he made the following predictions about time dilation in clocks rotating on the Earth's surface: 1) Time Dilation due to velocity: "If one of two synchronous clocks at A is moved in a closed curve with constant velocity until it returns to A, the journey lasting t seconds, then by the clock which has remained at rest the traveled clock on its arrival at A will be 1/ 2 t v2/c2 second slow. Thence we conclude that a balance-clock at the equator must go more slowly, by a very small amount, than a precisely similar clock situated at one of the poles under otherwise identical conditions. See " On the Electrodynamics of Moving Bodies p. 11. 2)
No preferred frames of reference: "On the basis of the empirically
known properties of the gravitational field, the definition of the
inertial frame thus proves to be weak. The conclusion is obvious that
any arbitrarily moved frame of reference is equivalent to any other for
the formulation of the laws of Nature, that there are thus no
physically preferred states of motion at all in respect of regions of
finite extension (general relativity principle)." See Einstein's Nobel prize lecture
of 1921, P. 486.
3) Time dilation due to acceleration or gravitation: "Let K be an inertial frame without a gravitational field, K’ a system of coordinates accelerated uniformly relative to K. The behaviour of material points relative to K’ is the same as if K’ were an inertial frame in respect of which a homogeneous gravitational field exists." "We shall now determine the relation between the time r and the local time s of a point event... s = t (1+ g e/ c2)." Where g is the acceleration and e is the distance along the x-axis. From Einstein's "On the Relativity Principle and the Conclusions drawn from it" (1907). P. 305. Our webapp simulating the Hafele and Keating experiment is here with the experimental conditions pre-loaded, and using the method that they describe in their two Science articles from 1972. This can be compared and contrasted with the Ashby calculation mentioned earlier, although they both arrive at the same values. The result from the simulator is a little different from the experimental result of HK, since the simulator must assume straight flight for a given duration and altitude, whereas in the real experiment these values were summed over the actual flight path, which was a little different. This is discussed at the Hyperphysics educational website here, where the plug-in and real results are discussed in detail. Using this simulator, one can modify the experimental conditions to examine how it would alter the final outcome. In
light of what we have discussed in the previous chapter, we can say
that Einstein's prediction in 1) of 1905 ends up being wrong, because
it does not anticipate his later discovery of 3) in 1907. When 1) and
3) are considered together, Hafele and Keating
prove that Einstein's predictions are correct, but only if the
hypothesis that time dilation is approximately constant at sea level
(on the geoid)
is true, as appears to have now been confirmed. However, this leaves
2), which is where Einstein's theory of relativity begins to falter
when it comes to time dilation on the earth. We have to consider Hafele
and Keating's opening statement that their experiment is a resolution
of the twins paradox. From the tenets of relativity, there are no
physically preferred states of motion - as Dingle aptly pointed out: "According
to the restricted theory of relativity, a moving clock runs slow
compared with a stationary one. Hence, if we regard M as moving, his
clock will be behind R's when they reunite. But the principle of
relativity allows us with equal justification to suppose that R is
moving and M is stationary, and in this case M's clock will be ahead of
R's when they reunite. These results cannot both be true. Which then,
if either, is right? " The
problem is that from the perspective of the observer on the ground, the
moving " clocks" of Hafele and Keating have
experienced identical motions with respect to the stationary clock on
the ground. If their motions were truly "relative", then both should
arrive back at the starting point having experienced the same amount of
time dilation in the same direction. And as Dingle has stated, if the
motion is truly relative, then the ground clock could perceive the
moved clocks as either faster or slower. The fact that of the two moved
clocks one increased in time and the other decreased, and this was the
only, definitive result, means that the entire effect is dependent on
the motion of some other reference frame, which is preferred over the
other three. Regardless of the protests of relativists that earth's
surface is a non-inertial frame and thus the rules of special
relativity do not apply, we must acknowledge that in the Hafele and
Keating experiment, one twin definitely experiences a speeding up of
his clock, and the other a slowing down, and from their motions alone,
they can determine their velocities with respect to what can only be
defined as a preferred frame, the non-rotating, geocentric (ECI) frame of the earth. This is
similar to the common usage of the Cosmic microwave background (CMB)
radiation as a reference frame for all cosmological motion - preferred
frames have crept into modern physics despite the protests of
relativists, even though the very concept is antithetical to the
originating concept of relativity - "that there are no preferred states
of motion at all". Even the Australian Department of Defense
has
found it appropriate to release to the public their internal research
reports critical of relativity, and in favor of an ether-based
treatment of space and time measurement, see here. As
Murray pointed out, Hafele and Keating were following a revised form
of relativity attributable to Builder, who they reference in their
first paper in 1971. In Builder's "Ether and Relativity" he
summarizes his revised view as follows:
"The
relative retardation of clocks, predicted by the restricted theory of
relativity, demands our recognition of the causal significance of
absolute velocities. This demand is also implied by the relativistic
equations of electrodynamics and even by the formulation of the
restricted theory itself. The observable effects of absolute
accelerations and of absolute velocities must be ascribed to
interaction of bodies and physical systems with some absolute inertial
system. We have no alternative but to identify this absolute system
with the universe. Thus in the context of physics, absolute motion must
be understood to mean motion relative to the universe, and any wider or
more abstract interpretation of the "absolute" must be denied.
Interactions of bodies and physical systems with the universe cannot be
described in terms of Mach's hypothesis, since this is untenable. There
is therefore no alternative to the ether hypothesis. " Builder
thus concludes that there must exist "an absolute inertial system"
which is the universe itself, and in doing so is effectively
re-introducing the preferred ether frame of Lorentz back into
relativity, the very thing which Einstein sought to eliminate.
Surprisingly, Paul Langevin made similar
suggestions in 1911. From this standpoint, the Hafele and Keating
experiment might better be interpreted using Lorentzian Ether Theory
(LET), since the result of the experiment can best be understood in
terms of a preferred geocentric inertial frame. We shy away from the
name "Lorentzian Relativity", since, as Dingle correctly pointed out: "despite
the name "relativity theory" given to it, Lorentz's theory was not,
strictly speaking, a relativity theory at all; that is to say, it did
not regard the relative motion of two bodies as, with equal validity,
divisible between them in any of the various conceivable ways; each
body had its own absolute motion - i.e. with respect to the ether - and
although we had not discovered how to find what that was, it was
nevertheless real." Science at the Crossroads P.130 But if we are to accept Builder's hypothesis of preferred frames, and in particular, a universal preferred frame for motion, an ether, then we must also accept the other critical tenet of Lorentz over Einstein, that it is the speed of light, and not time, which is the fundamental variable in our universe. In doing so, we must completely re-consider the notion of Einstein's 4D space-time. This is because in accepting a notion of absolute motion, or a preferred frame, we are as Dingle says, rejecting the notion of "relative motion". Despite Einstein borrowing heavily from Lorentz's equations and theory, and the fact that both theories predict similar results for the same experiments, the two theories are philosophically antithetical - and as such the conclusions about the nature of space and time result in entirely different models of the universe.
Why
does Gravitational Acceleration lead to Time Dilation? From
the foregoing, we are led to the concept of a universal frame of
reference for motion, an "ether" as suggested by Builder, and in the words of Dingle,
although we haven't discovered what it is, it is nevertheless real. Let
us consider then that gravity is like a pressure difference across this
frame, a pressure difference in and of space, rather than a gradient in
time. If space were a medium, then the speed of sound in that medium
would vary across space according to this pressure. Similarly, we could
consider that real space behaves as if there is a difference in some
velocity effect at height h above earth vs. sea level due to this
pressure difference. The acceleration due to gravity at 9.8m/s2
corresponds to this velocity gradient with height. As will be shown
herein, this velocity gradient could be conceived of as the difference
in the speed of light with altitude. Just like in our model of space as
a medium, the velocity of sound in that medium would differ at
different pressures corresponding to different heights. Consider
that we experience a gravitational time dilation at the sea level
surface of the earth that is equivalent to a factor of 6.96928E-10 as
compared to some large distance away from the earth, as has been
accepted in Terrestrial Time(TT).
If we translate this value into the equivalent velocity for
velocity time dilation of the same magnitude using Einstein's
own
second order velocity time dilation equation,
we get: 6.96928E-10
= v2/2c2
v2 = 6.969E-10 * 2c2
v = 11180.34 m/s
v<<c This implies that the speed of light at the surface of the earth may be slower than far out in space, althought this value for v interpreted as a difference in the speed of light between the two is is likely far too high (as will be discussed shortly) . Referring to Maxwell's concept of space as being a medium in his discovery of electromagnetic radiation:
Since
the medium is incompressible, and u corresponds to the density, the
only factor that can change when the speed of light changes is the
electric permittivity Eo, which corresponds to the inverse shear
modulus or inverse pressure/transverse elasticity of a medium capable
of supporting transverse waves. The product Eo* u in far space should be less than that at the earth's surface and Eo alone should account for this amount, since the density should remain the same. This would suggest that if a property of space changes with gravity, it might be detectable as a change in the electric permittivity of the vacuum. We note that although the difference in the speed of light would have to be real, since Lorentzian ether theory calls for clocks to mechanically slow when the speed of light slows, and rods shorten when they have a velocity relative to a preferred frame, the Lorentz transformations will make this difference in the speed of light invisible to the local observer, and thus the speed of light will still be measured to be the same at all altitudes. Gravitational time dilation would then be the only clear evidence that the speed of light is changing velocity with height. How Einstein arrived at the Equivalence principle
for Time Dilation: Is it possible to derive this velocity relationship to gravity from the known equations? Let's examine how Einstein made the mental leap from velocity time dilation to gravitational time dilation. We refer to Einstein's 1907 paper "On the Relativity Principle and the Conclusions Drawn from it" P. 305: Definitions: g = acceleration S = reference system S = reference system uniformly accelerated along x-axis with respect to S S' = a reference system that coincides with S at time t' in S'. Coordinates of a point event occurring at t' are: x' = e = h y' = h z' = z The clock in S is set to match S' at t'. The readings on clock in S match the readings on clock S' for the time element t. Relative to S, light propagates at C during the time element t. Events in S' are simultaneous with events in S, since S' is momentarily are rest with respect to it. First, the clocks of S are adjusted to be synchronous with the clocks in S at time t=0. s is the local time in system S. t is a time element in system S . We shall now determine the relation between the time t and the local time s of a point event. For the local time interval s2- s1 in system S, g = d/t2, since v = d/t, so g = v/t, so v = g t if two events are simultaneous when t1-
v/c2 x1 = t2-
v/c2 x2 then t2- t1 = v/c2 * (x2 - x1)
(x2 - x1) = h t1 = t and t2 = s. v = g t substituting, then
s =
t (1+ g h/ c2) which is the gravitational time dilation term However, the relationship gh/c2 can be taken to be equivalent to the velocity time dilation equation v2/2c2 when v<<c, if we want to express gravitational time dilation in terms of velocity time dilation. We find that g h can then be expressed as a velocity as follows: v = (2gh) 1/2, and g = v2/2h . A Lorentzian Interpretation of Einstein's Principle
of Equivalence: (updated
Nov. 5th, 2013) From a Lorentzian perspective, time dilation due to acceleration can be viewed as being due only to the velocity itself, as is also consistent with the clock hypothesis of relativity. As dissected out above, for an acceleration of g , this corresponds to a velocity by the relation: g = v2/2h
the velocity difference over distance h is equal to v , where the start velocity vo is zero. This is because: g = (v- vo)/t. If g = 10m/s2, and t = 10 seconds, then v- vo = 100-0 = 100
The average velocity is (v- vo)/2 = 50 m/s d = vavg * t = 50*10 = 500m. g = 1002/(2*500) = 10 m/s2 = v2/2h
If this relationship is considered consistent with gravitational acceleration, then the same equation may be applied to it. In this model clocks at altitude h run faster than clocks at the surface, because the speed of light is faster at altitude h by some amount related to this value v. Only apparent time changes, not absolute time, due to the error introduced in the clock by the difference in the speed of light in the clocks at different altuitudes. . Knowing the gravitational acceleration g, and the height h, the value v can be determined. For example: g = 9.798 m/s2, and h = 10,000 m , g = v2/2h thus v = 442.68 m/s. If we then plug v into the Lorentz transformation equation: Dt = 1-(1-v2/c2) 1/2 = 1.0902E-12 Lorentz method Dt = gh/c2 = 1.0902E-12 Einstein method The two equations then agree on the rate change for a caesium clock at altitude h compared to sea level. 1-(1-v2/c2) 1/2 = 1-(1-2gh/c2) 1/2 = gh/c2 = v2/2c2 when v<<c. The question then is, how does this predicted value for v for the equivalent velocity time dilation relate to the expected hidden speed of light difference between the surface and height h called for by Lorentz's treatment? Calculation of the Predicted Speed of Light Difference with h on Earth:
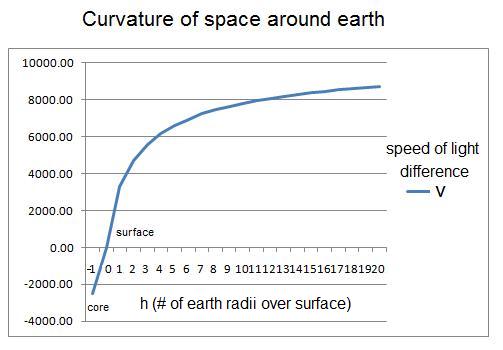
Using the equations developed herein for the properties of space above and below the surface of the earth, we can calculate how space might be curved in velocity:
In example 1, we see what will happen if we make gh/c2 = v2/2c2 and pre-suppose that v in this case corresponds to the difference in the speed of light at different altitudes: Example 1: At height h above the surface, v = (2GM/(r+h)) 1/2 where r is earth's radius and h is the height above the surface in meters. At the core of the earth, v = ( 2* 3/2*GM/r) 1/2
Everywhere on this curve, for a given v, v2/2c2 = gh/c2 .where v<<c.
This method appears to exaggerate the speed of light difference. If such a difference did exist, it would become obvious in GPS propagation time measurements. We now consider the problem another way, as in example 2 below:
Example 2: If we consider two clocks, one at the surface of the earth, and another at an altitude h, and each is used to measure the speed of light in its locality, they would both measure a velocity of c. However, if the clock at the surface was used to measure the speed of light at altitude h instead, we would expect that since it is counting slower than the clock at altitude h, it would measure the speed of light at altitude h as being: = C' * (1+ gh/C'^2), where C' is the speed of light at the earth's surface.
The measured speed of light difference Vdiff between the surface and altitude h would then be:
Vdiff = C' * (1+ gh/C'^2) - C'. or simply Vdiff = gh/C' This means that Vdiff = v^2/2C' , or Vdiff = C'*(1-SQRT(1-v^2/C'^2)
Vdiff = how must faster the speed of light is at height h, with respect to the speed of light at the surface, both measured with a hypothetical clock counting absolute time at h = 0. v is the relative velocity necessary to cause the equivalent velocity time dilation. We could presuppose that the clock at height h is synchonized with the clock at height 0. Curvature of Space Around Earth in Velocity
To determine the change in Eo with height h, the equations are: Eo = 1/(C'2u ) for sea level, and Eo = 1/((C' +gh/c)^2 *u) at height h. The difference between Eo at the surface and Eo in distant space (say 100 eath radii away) is then: assuming Vdiff = 0.874 m/s
Surface Eo = 8.85418796866E-12 Distant space = 8.85418791701E-12 Difference = 0.9999999941669 of surface
When expressed as a gravitational potential instead as in the manner of Einstein, the curve is as below:
All scenarios form wells - the Lorentz scenario is a well in the medium of 3D space, whereas the Einstein version is a well in the medium of 4D space-time, similar to the picture below:
Conclusions: The purpose of this exercise was to examine how time dilation might be understood as purely a velocity effect, based on our projection of what the Lorentzian interpretation would be, rather than the more common one of Einstein. From this Lorentzian perspective, apparent time dilation depends only on the velocity of light with respect to the measuring clock. If the clock is moving with respect to a preferred frame of reference, then the clock will slow because the speed of light in the clock is c-v, where c is the speed of light in the preferred frame. This explains velocity time dilation. If the speed of light in two preferred frames are different, due to some difference in the properties of the medium of space at the two points, then the time dilation reflects the difference between the speed of light in the two frames. Dt is proportional to Dv. This implies that the rate of acceleration due to gravity directly corresponds to the rate of change in the speed of light across space, due to changes in the nature of space in the gravitational field. Space is curved, rather than space-time. What is defined as a "preferred frame" then becomes more difficult - the speed of light becomes a function of the properties of space (u, a constant) and (Eo, permittivity, a variable) at any given point- the clock rate then depends on the local Eo* u and the velocity of the clock with respect to it. References: 1. Ashby, Neil, Relativity in the Global Positioning System. 2007 2. Bailey
et al., “Measurements of relativistic time dilation for positive and
negative muons in a circular orbit,” Nature 268
(July 28, 1977) pg 301. Bailey
et al., Nuclear Physics B 150 pg 1–79 (1979).
3. Builder, G., Ether and Relativity. 1957. 4. Dingle, Herbert, The Resolution of the Clock Paradox. 1957 5. Dingle, Herbert, Science at the Crossroads, 1972. 6. Edgar, R.S., Field Analysis and Potential Theory. 1994. 7. Einstein, A., (1905) On the Electrodynamics of Moving Bodies. 8. Einstein, A., (1907) On the Relativity Principle and the Conclusions Drawn from it 9. Hafele, J.C., Keating, Richard C., "Around the World Atomic Clocks". Science 177, 166-170. 10. Murray, W.A. Scott, "If you want to know the time..." Wireless World. 92 No.16 28-31 1986. 11. Sherwin, “Some Recent Experimental Tests of the 'Clock Paradox'”, Phys. Rev. 129 no. 1 (1960), pg 17.
|