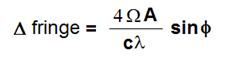The Michelson-Gale Experiment Doug Marett (2010) a .pdf version of
this paper is available here
In 1904, Albert Michelson conceived
of an experiment to detect the relative motion of the earth and the
ether [1]. His primary goal was to design an experiment to determine if
light is entrained by the rotation of the earth, in other words, does a
preferred frame of reference for light rotate with the earth or not? He considered an
experiment where it might be possible to send two beams of light in
opposite directions around the earth at the equator. He argued that if
the light beams are not entrained by the rotation of the earth, then
one beam would be faster and the other slower, in proportion to the
rotational velocity of the earth. He also conceived that the velocity
difference would be proportional to "the length of the parallel of the
latitude at the place.", in other words, the velocity difference would
decrease as one went higher in latitude. A measurement of time
difference for each beam to return to the start would then be a measure
of the amount of entrainment due to the rotation of the earth.
In refining his argument, he proposed that it was
not necessary for the light to go all the way around the globe - since
there should be a velocity difference for any closed path rotating on
the surface of the earth. He presented the following equation to
calculate the time difference expected, using the shift in the
interference fringes when the two beams overlap at the detector as a
measure of the time difference:
Fig.1: 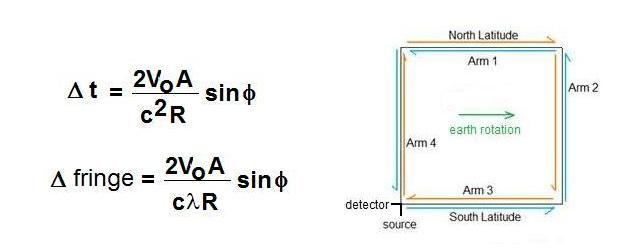
where: Vo = the tangential velocity of the earth's rotation at the equator (465m/s) A = the area of the circular path R = the radius of the earth (6371000 m) c = speed of light (3E8 m/s) f = the latitude in degrees where the experiment is conducted. l = wavelength of the light The experiment remained in abeyance for several years, until Silberstein published a paper in 1921 on the theory of light propagation in rotating systems [2]. In this article, Silberstein discusses Michelson's proposed experiment and through calculations of his own demonstrated that the time difference expected in such an experiment would be double what Michelson suggested. Silberstein's calculation proceeds somewhat differently than Michelson's. First he uses the scalar angular velocity of the Earth, which he defines as: w = u/R, where R is the radius of the earth. u is the velocity of the earth at the surface. So at 41deg. 46', the velocity u = 346.83 m/s, then the scalar velocity w = 346.83/6371000m = 5.4439E-5 m/s Silberstein explained how to proceed with the calculation as follows: Let's say we have a system S in rotation. On a particular element of the path S, we have a distance ds. For rotation in the positive direction, we have the time taken to traverse the element as ds/c * (1-us/c). This gives a path retardation of - 1 /c2 us ds . However, during rotation the paths of the light beams are actually curved, and because of this the area enclosed by a positive and negative path is different. After taking all these factors into account, the expected fringe shift becomes:
where W is the angular velocity of the earth at the equator, so Wsinf is the angular velocity of the earth at the latitude of measurement. When the expression Wsinf is replaced simply with W, where W becomes simply the angular velocity experienced the interferometer along its sensitive axis, then we have:
which is the most common expression for the fringe shift due to a Sagnac interferometer in use today. In returning to the latitude effect, this is best described with the aid of a diagram (figure 2 below): Fig.2: The proposed experiment of Michelson should then be treated as a Sagnac interferometer with its axis of spin (herein referred to as the z axis) oriented vertically with respect to the earth's surface. If the interferometer is at the North pole, it experiences the full earth's rotation of 15 degrees per hour. However, if it is at the equator, the z-axis is perpendicular to the axis of rotation of the earth, and thus the device does not experience a rotation at all along its sensitive axis. If the device is at 45 deg. latitude, then it experiences an intermediate rotation rate of Wsin(45). The z-axis of the interferometer can also point N-S or E-W, as shown in the above figure. When oriented N-S, the angular velocity experienced by the interferometer is Wcos(45), the opposite of the first example. If the z-axis is oriented E-W, then the z-axis is perpendicular to the rotational axis of the earth in all positions, and thereby no angular velocity is experienced by the sensitive axis of the device. After the urgent insistence of Silberstein that the experiment should be conducted to answer the question of rotational drag of the ether, Michelson began work on the apparatus. An initial test at mount Wilson in the open air was too unstable to get a reading of the fringe shift, so it was decided to lay an evacuated pipeline at Clearing, Illinois, 2010 feet (612.65 m) long E to W by 1113 ft (339.24 m) long N-S. Due to the difficulty of obtaining a zero reading for the device, a second path with a much shorter E-W length was laid as a control. The latitude for Clearing, Illinois is 41 deg. 46', thus the latitudinal angular velocity was Vo/R x sin (41+46/60), where Vo = 346.83 m/s. The experimental arrangement is described in detail here [3]. Parameters for the calculation: Angular velocity of the earth at the equator W =tangential velocity at equator / Radius of earth in meters = 465/6371000 = 7.2987E-5 = W Area of the Michelson-Gale interferometer = (612.65m*339.24m) = 207,840 m2 = A. Latitude = 41 degrees 46'. The equation for a Sagnac interferometer is: Dfringe = 4* W*A*sin(latitude) /(C*l) The expected fringe shift is then: Dfringe = 4*(465/6371000)*sin(41o+46/60o)*(612.65m*339.24m)/(3E8*5.7E-7) Dfringe = 0.2364 In our Michelson-Gale simulator, the calculation is shown in an interactive format. Michelson and Gale use a slightly different calculation method in part I of the series of papers [4] to estimate the expected result if there was no ether drag, which attempted to retain his original ideas about the differing velocities and path lengths dependent on the latitude of the experiment, and the latitudes of each arm. His equation replaces the area A with the length of the affected side L*h, where h is the tangential velocity of the earth experienced by the length. In this way the resulting equation is similar to Ruyong Wang's Dt = 2vl/c2 and Dfringe = 2vl/cl expressions for the linear FOG [5]. The result of the experiment when it was finally conducted in 1925 was that the measured fringe shift was found to be 0.230 +/- 0.005, which was found to agree with the prediction of no ether drag by rotation within the experimental error. What this means is that the speed of light is constant in the non-rotating frame, a result that is consistent with Lorentz Ether Theory. Theories that propose that the Earth Centered Inertial Frame (ECI Frame) is a preferred frame for the speed of light also are consistent with this result, since the speed of light in this experiment is constant in the ECI frame of the earth. The explanation of the result using relativity becomes somewhat more complicated, see for example [9]. The inequality of the measured speed of light in the two directions by the observer moving with the interferometer (in the ECEF frame) would appear to violate the second postulate of special relativity, but relativists generally argue that special relativity provides no comment on rotational frames of reference so it actually does not apply, and one would have to use general relativity to attempt to explain it. As A.G. Kelly points out, there is no such thing as a perfect inertial frame - almost all motions in the universe involve some degree of rotation. In this way rotational frames have been considered inertial frames by some relativistic researchers, even though their degree of rotation has been much higher than other rotational frames that have been labelled outside the jurisdiction of special relativity.[6] Wang has also showed that when the Sagnac interferometer's rotation is made effectively linear motion using a fiber optic conveyor (FOC) the effect is identical.[5] Klauber [7] has also argued that the speed of light difference on the rotating Sagnac interferometer are real, since they are measured with local clocks and rods, and lead to the paradox that when using Einstein synchronization on the rotating rim a clock becomes out of synchronization with itself. The paradox is resolved by assuming the speed of light varies on the rim of the disk. To quote Klauber: "Anyone can determine their angular velocity and their circumferential velocity (wr) relative to the inertial frame in which their axis of rotation is fixed. When light rays are used to synchronize clocks around the circumference by observers knowing their circumferential velocity and the speed of light from (1) above, the synchronization turns out to be exactly what one finds by using light rays from a clock located at the disk center. Hence, a clock can be synchronized with itself using light rays traveling around the circumference and there is no paradox at all. It is
interesting to note that the speed of light in a Sagnac interferometer
is only constant with respect to the laboratory frame (on the earth) if
its z-axis is pointing E-W and thereby the sensitive axis is
perpendicular to all motion. In all other orientations, the device is
sensitive to the diurnal rotation of the earth to some degree, and it
is even sensitive to the rotation of the earth around the sun, an
effect 365 times smaller. In this way the Michelson-Gale experiment,
and Sagnac interferometers in general, give a contradictory result to
all other interferometer experiments that take the laboratory frame as
an inertial frame and have assumed that light speed is isotropic in
that frame. The inability of these latter experiments to detect their
own translational motion through space has already been adequately
explained using the Lorentz transformations, which apply, as Lorentz
intended, to preferred frames just as Einstein has applied them
relative frames, the only difference being a change in convention about
clock synchronization. [8] It
is sometimes said that the Sagnac interferometer detects rotation with
respect to the fixed stars - this is difficult to distinguish from the
idea that
the Sagnac interferometer detects rotation with respect to the
non-rotating gravitational frame of the earth (Earth Centered Inertial,
ECI frmae) that is considered to be non-rotating with respect to the
fixed stars. It has been demonstrated experimentally that Ring
Laser gyroscopes, the cousin of the fiber optic gyroscope,
detects the sidereal day rotation rather than the 24 hour day
rotation.(10). This latter observation is important but is incapable of
distinguishing whether the ECI frame or sidereal space is
static
frame that the Sagnac rotation is measured against. References: 1). A. Michelson, (1904) "Relative Motion of Earth and Aether." Philosophical Magazine (6), 8, 716-719. 2) Ludwik Silberstein (1921) "The Propagation of Light in Rotating Systems." JOSA Vol. 5, No. 4, p. 291-307. 3) Albert Michelson, Henry Gale (1925) The Effect of the Earth's Rotation on the Velocity of Light. Part II. 4) Albert Michelson, Henry Gale (1925) The Effect of the Earth's Rotation on the Velocity of Light. Part I. 5) Wang, Ruyong, (2003) "Modified Sagnac Experiment for Measuring the Travel-Time Difference between Counter-propagating light beams in a uniformly moving fiber. Phys. Lett. A 312, 7-10. 6) A.G. Kelly "The
Sagnac Effect and Uniform Motion." 7) Kauber, Robert, 1999 "Relativistically Rotating Frames and Non-time-orthogonality." 8) Mansouri, R., Sexl, R. (1977) "A test theory of Special Relativity: II First Order Tests." General Relativity and Gravity Vol. 8 No. 7, pp.515-23. 9) http://arxiv.org/abs/gr-qc/0305084 10)
Schreiber, et.al., Direct Measurement of diurnal polar motion
by ring laser gyroscopes (2003) http://cds.cern.ch/record/749229/files/0406156.pdf
Other articles of interest on the Sagnac Effect by Doug Marett: 10) Doug Marett (2015) Single Mode Fiber Optic Sagnac Interferometer with Wireless Data Collection - Vixra e-print archive 1506.0002 11) Doug Marett (2010) How to Build a Sagnac Interferometer / Fiber Optic Gyroscope (FOG) 12) Doug Marett (2011) Detecting Earth's rotation Through Space Using a Large Area Sagnac Interferometer - article here 13) Doug Marett (2012, 2015) The Sagnac Effect: Does it Contradict Relativity? General Science Journal 5993. |