Spacetime-
Right or Wrong?
Doug
Marett 2013
Einstein’s concept for space-time calls for 4
dimensions of space, three
for physical dimensions of space (x,y,z) and one for time (t). The idea
is that
time is a dimension in the sense that the past, present and future
coexist – so
different places in time can be defined by simply giving them a
coordinate on
this space-time dimension. Let’s take the example of the twins paradox.
The stay
on earth twin (A) has the space-time coordinates x,y,z,t. The twin that
leaves
the earth on a rocket whose clock initially counted at the same rate as
twin A,
now has his clock slow due to his velocity v. Thus after some interval
in time
the traveling twin B has moved in space to a new coordinate x’,y’,z’,
but since
his clock is now counting slower, he is not in the same time frame as
twin A,
so at any given time t for twin A, twin B is at some different time ,
which we
will call t’.

The
obvious implication is that twin B
and his rocket are not only in a different time coordinate that twin A,
but are
also experiencing time moving more slowly than twin A. Stopwatches held
by both
twin A and B would count at different rates. If what Einstein proposed
is true,
we can only conclude that the physical environment of the rocket and
twin B is
distinct from that of twin A in that they do not share the same rate of
real time.
Is there any way to test this? One conclusion that logically comes up
is that
if both twin A and twin B measure the speed of light in their own
frames, they
will measure them as both being C=C’ = 3E8 m/s. However, if they arrive
at the
same answer using two stopwatches that are obviously counting at
different
rates, then C cannot = C’ if both are measured by the same
stopwatch. This
would seem
to be a contradiction to the constant speed of light hypothesis. Is
there
something wrong here? Let’s look at one of the most popular
explanations for
how time dilation occurs using the light clock analogy, and then
proceed to a
thought experiment test of this idea.
The
Light Clock Analogy
When we see a supernova explode in the sky, we do
not say “that event
just happened”, since we know the light from that event has taken
perhaps
thousands of years to reach us from some distant point in space. We
would say,
rather, that the explosion happened thousands of years ago. This is
because our
judgement of the simultaneity of events is independent of the speed of
light.
Rather the speed of light might be used to insinuate when an event
could have
happened in the past, based on the propagation delay. So why then would
we believe
that the rate of time itself depends on the speed of light? Consider
Einstein’s
analogy, often reproduced, of a light beam bouncing between two
mirrors. In his
analogy, two horizontal
mirrors face each other and one mirror is spaced above the other by a
distance
d. A light pulse bounces vertically between the two mirrors as shown on
the
left. The time it
takes for the pulse of
light to do a round trip (from the top mirror to the bottom and back)
is twice
the distance d divided by the speed of light. This is his light clock.
One tick
is one return bounce of the light beam.

Suppose
the "light
clock" were traveling sideways at a very high (but constant) speed of
0.5
C. Now the pulse would follow the "saw tooth" path shown on the right
side of the drawing. Since light speed is the same as before (remember,
the
speed of light is not changed by the speed of its source), it will take
longer
to make a round trip. So our "light clock" takes longer to count out
its intervals. Another way of saying this is that the clock "ticks"
more slowly.
But
here lies the problem. This analogy works because the speed of light is
constant as seen by observer A. From his vantage point, he can see both
clocks
working, and although the speed of light is travelling at the same rate
in
scenario 2, it has taken a longer path to hit the moving mirrors. In
taking a
longer path, it has taken more time to reach the end. But because we
have
already said that the rate of time is independent of the speed of
light, we
cannot assume that “real” time has passed slower for observer B than
observer
A, we can only conclude that B’s clock has counted mechanically slower
because
it has taken longer for the light to travel the distance between
scenario 2’s
mirrors. Now, if observer B measures the speed of light in his moving
frame
using “real” time, i.e. a clock not
affected by the speed of light, he should conclude that the
speed of light is
slower than C. Observer B is unaware that he is moving, so he perceives
the
mirrors to be opposite each other and separated by distance d, so he
would
measure the speed of light to be less than C. He is unaware that from
the perspective
of observer A, the path d has lengthened. So why does he conclude that
the
speed of light is instead C? This is because he measures the time
elapsed using
a clock that is based on the length of time it takes for light to pass
between
his own moving mirrors. In effect, his moving clock is calibrated by
the speed
of light seen in his own frame (which is 0.866*C), so consequently, his
clock
counts slower by exactly this amount (t/0.866). This makes him falsely
measure
that the light beam to have arrived at velocity C rather than C *
0.866.
Since
the slowing
of clocks (apparent time dilation) does occur in reality, this implies
that the
speed of light is only actually C in the stationary frame, and in the
moving
frame it is actually C *
0.866,
but is erroneously measured as being C in his frame due to the slowing
error
introduced into his moving clock by the longer light path.
If
the slowing down
of a clock due to a velocity is possibly just an illusion, and real
time is
unaffected, then perhaps space-time also doesn’t exist in the way
Einstein
conceived of it. From this revelation we can propose the following
conclusion:
The
moving frame is not a
physical entity with a distinct time t’ ; it is instead only a perspective.
What
kind of experiment could
we perform to test this idea? Let’s return to the light clock analogy,
but this
time lets propose to send a laser beam through the stationary observers
frame
and also the moving observer’s frame together as part of the same light
path. If
what Einstein says is true, and the moving observer exists in a
timeframe
distinct from the stationary observer, then the beam returning to the
stationary observer through the moving frame should have travelled at
some speed
slower than C. This is because, as we said earlier, we are now
measuring C and
C’ with a single stopwatch.
Below
is a diagram of the
thought experiment. Observer A in the stationary frame fires a laser
beam into
the moving frame, bouncing off the moving mirrors, and then returns
back to his
original position, where he measures the elapsed time. Since we know
from every
laser experiment performed to date that the measured speed of light
will always
be C, he has no choice but to conclude that the measured speed of light
is still C
based on the distance traveled by
the beam in his frame.
Light
path as observed from the stationary frame by observer A:
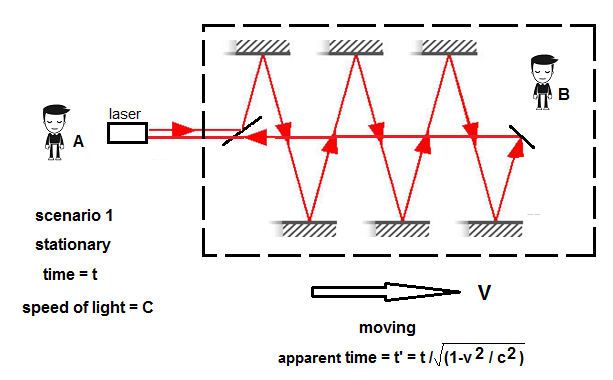
The
speed of light has not
miraculously changed its speed inside of the moving frame, because the
frame in
motion does not drag its own time with it. The characteristics and rate
of time
are exactly the same in the stationary frame as in the moving frame -
the
difference is the lack of agreement by the observers on the distance travelled by the beam of light
from each perspective. Observer
B simply
sees the beam travel a different path than observer A:
Apparent
path traveled by light as seen by the moving observer B:

The
same is true for the
stationary and moving clocks –since the clock rates are geared to the
speed of
light, each clock counts at a different rate because the beam of light
has
traveled a different distance from each clock’s
perspective. Real time has not changed. This matches the
known experimental
results if and only if the real speed of light is constant in a single
frame of
reference, the stationary frame. All
other conclusions about the speed of light in the moving frame and the
rate of
time are illusions caused by the motion of the frame with respect to
the
preferred, stationary frame for the light beam.
What
we can conclude from
this exercise is that the slowing of a clock on a rocket ship is
meaningless
and does not imply that the rate of real time has changed in any frame
of
reference. It is simply an error of perspective experienced by both the
moving
observer and the moving clock, in exactly the way that was proposed by
Larmor in
1901. This argument should apply to atomic clocks that have been most
commonly
used to demonstrate time dilation, since a slowing of the speed of
light from
the perspective of a moving atom should lead to a change in the
frequency of
emission of the atom. This was in fact the thesis of Herbert Ives when
he
performed the Ives and Stillwell experiment (Transverse Doppler effect
in Canal
rays), and he himself states explicitly that he was attempting to prove
the
theory of Larmor and Lorentz, not Einstein.
But this is not
the only reason why Einstein’s
concept of space-time must be wrong. What space-time implies is that
all
events, past, present and future, are already written in the fabric of
space.
Such a conclusion relegates all human activity to simply being
automatons
acting out the frames of a preordained film strip. If we were to
believe
Einstein we would have to believe that there is no
free will at all. That in and of itself should be reason
enough
to reject the space-time concept without further consideration!
